
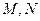 是椭圆
是椭圆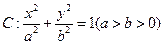 上关于原点
上关于原点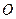 对称的两个点,点
对称的两个点,点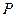 是椭圆
是椭圆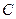 上任意一点,且直线
上任意一点,且直线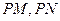 的斜率都存在(记为
的斜率都存在(记为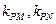 ),则
),则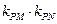 是与点
是与点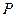 位置无关的定值。试写出双曲线
位置无关的定值。试写出双曲线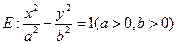 的类似性质,并加以证明。
的类似性质,并加以证明。 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:不详 题型:解答题
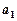 ,
,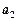
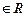 ,
,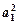
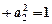 ,则
,则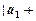
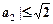 .”可以如下证明:构造函数
.”可以如下证明:构造函数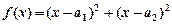 ,则
,则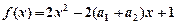 ,因为对一切
,因为对一切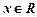 ,恒有
,恒有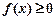 ,所以
,所以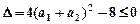 ,故得
,故得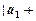
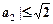 .
.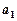 ,
,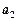 ,
,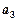
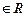 ,
,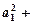
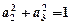 ,求证
,求证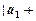
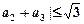 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 边形
边形 中的每条边和每条对角线都被染为n种颜色中的一种颜色.问:对怎样的n,存在一种染色方式,使得对于这n种颜色中的任何3种不同颜色,都能找到一个三角形,其顶点为多边形
中的每条边和每条对角线都被染为n种颜色中的一种颜色.问:对怎样的n,存在一种染色方式,使得对于这n种颜色中的任何3种不同颜色,都能找到一个三角形,其顶点为多边形 的顶点,且它的3条边分别被染为这3种颜色?
的顶点,且它的3条边分别被染为这3种颜色?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x2 |
| a2 |
| y2 |
| b2 |
| F2M |
| MP |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| F2M |
| MP |

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 出发依次沿图中线段到达
出发依次沿图中线段到达 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 各点,最后又回到
各点,最后又回到 (如图所示),其中:
(如图所示),其中: ,
, ,
,
 .欲知此质点所走路程,至少需要测量
.欲知此质点所走路程,至少需要测量 条线段的长度,
条线段的长度, ( )
( )A. | B. | C. | D. |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com