
| 优分 | 非优分 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 | 50 |
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
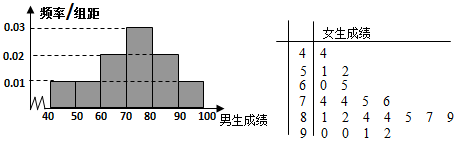
分析 (Ⅰ)列出2×2列联表,计算k2的值,判断即可;(Ⅱ)根据优分人数X服从二项分布$B(3,\frac{2}{5})$,求出E(x)即可.
解答 解:(Ⅰ)根据图示,将2×2列联表补充完整如下:
| 优分 | 非优分 | 总计 | |
| 男生 | 9 | 21 | 30 |
| 女生 | 11 | 9 | 20 |
| 总计 | 20 | 30 | 50 |
| X | 0 | 1 | 2 | …(10分) 3 |
| p | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
点评 本题考查了2×2列联表,考查二项分布和数学期望,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抽签法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 随机数法 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com