
【题目】已知圆![]() ,定点
,定点![]() ,
,![]() 为圆上任意一点,线段
为圆上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() ,当点
,当点![]() 在圆上运动时,点
在圆上运动时,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过定点![]() 的直线交曲线
的直线交曲线![]() 于不同的两点
于不同的两点![]() ,
,![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间),且满足
之间),且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】(1) 已知函数![]() ,若
,若![]() ,则
,则![]() _____.
_____.
(2)等差数列{an}的前n项和为Sn,若a2=2,a11-a4=7,则S13=________.
(3)若命题“x∈R,使得x2+(a﹣1)x+1<0”是真命题,则实数a的取值范围是______.
(4)在△ABC中,tanA+tanB+![]() =
=![]() tanA·tanB,且sinA·cosA=
tanA·tanB,且sinA·cosA=![]() ,则此三角形为_______.
,则此三角形为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.
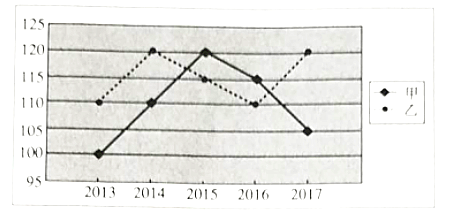
(1)根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;
(2)根据乙这五年年度体检血压值的数据,求年度体检血压值![]() 关于年份
关于年份![]() 的线性回归方程,并据此估计乙在2018年年度体检的血压值.
的线性回归方程,并据此估计乙在2018年年度体检的血压值.
(附: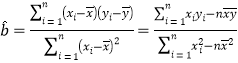 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥S-ABCD的底面为正方形,SD![]() 底面ABCD如下列结论中不正确的是 。
底面ABCD如下列结论中不正确的是 。
A. AB![]() SA
SA
B. BC//平面SAD
C. BC与SA所成的角等于AD与 SC所成的角
D. SA与平面SBD所成的角等于SC与平面SBD所成的角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com