
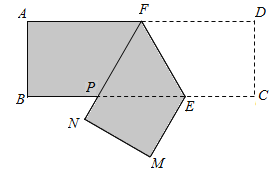
【题目】如图,某机械厂要将长![]() ,宽
,宽![]() 的长方形铁皮
的长方形铁皮![]() 进行裁剪.已知点
进行裁剪.已知点![]() 为
为![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,裁剪时先将四边形
上,裁剪时先将四边形![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 处(点
处(点![]() ,
,![]() 分别落在直线
分别落在直线![]() 下方点
下方点![]() ,
,![]() 处,
处,![]() 交边
交边![]() 于点
于点![]() ,再沿直线
,再沿直线![]() 裁剪.
裁剪.
(1)当![]() 时,试判断四边形
时,试判断四边形![]() 的形状,并求其面积;
的形状,并求其面积;
(2)若使裁剪得到的四边形![]() 面积最大,请给出裁剪方案,并说明理由.
面积最大,请给出裁剪方案,并说明理由.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),圆
是参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 与直线
与直线![]() 的交于
的交于![]() ,
,![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() ;对任意的
;对任意的![]() 、
、![]() ,
,![]() ,与
,与![]() 两数中至少有一个属于
两数中至少有一个属于![]() .
.
(1)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)证明:![]() ,且
,且![]() ;
;
(3)当![]() 时,若
时,若![]() ,求集合
,求集合![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时,![]() ,对任意
,对任意![]() R,均有
R,均有![]() .
.
(1)求证:![]() ;
;
(2)求证:对任意![]() R,恒有
R,恒有![]() ;
;
(3)求证:![]() 是R上的增函数;
是R上的增函数;
(4)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在距离为
,若存在距离为![]() 的两条直线
的两条直线![]() 和
和![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() ,则称函数
,则称函数![]() 有一个宽为
有一个宽为![]() 的通道.给出下列函数:①
的通道.给出下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中在区间
.其中在区间![]() 上通道宽度为1的函数由__________ (写出所有正确的序号).
上通道宽度为1的函数由__________ (写出所有正确的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴非负半轴为极轴建立极坐标系.
轴非负半轴为极轴建立极坐标系.
(1)写出曲线C的极坐标方程;
(2)设点M的极坐标为![]() ,过点M的直线
,过点M的直线![]() 与曲线C交于A、B两点,若
与曲线C交于A、B两点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与直线
两点,与直线![]() 交于
交于![]() 点,射线
点,射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为普及学生安全逃生知识与安全防护能力,某学校高一年级举办了安全知识与安全逃生能力竞赛,该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛,现将所有参赛选手参加笔试的成绩(得分均为整数,满分为![]() 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)求表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)按规定,预赛成绩不低于![]() 分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为
分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com