
【题目】已知函数f (x)=xlnx-x.
(1)设g(x)=f (x)+|x-a|,a∈R.e为自然对数的底数.
①当![]() 时,判断函数g(x)零点的个数;
时,判断函数g(x)零点的个数;
②![]() 时,求函数g(x)的最小值.
时,求函数g(x)的最小值.
(2)设0<m<n<1,求证:![]()
【答案】(1)① g(x)有且仅有两个零点.②a-e.(2)证明见解析
【解析】
(1)将![]() 代入g(x)=f (x)+|x-a|,化简得g(x)=xlnx+
代入g(x)=f (x)+|x-a|,化简得g(x)=xlnx+![]() ,再根据导数正负判断在极值点处函数值的正负,结合极值点两侧值加以论证即可,可取
,再根据导数正负判断在极值点处函数值的正负,结合极值点两侧值加以论证即可,可取![]() 验证求解
验证求解
(2)由于参数的不确定性,需根据![]() 将参数
将参数![]() 分成a≤
分成a≤![]() ,a≥e,
,a≥e,![]() <a<e三段进行讨论,进一步判断函数的单调区间
<a<e三段进行讨论,进一步判断函数的单调区间
(3)可先构造函数h(x)=![]() ,求得h′(x)=
,求得h′(x)= >0,于是h(x)在(0,1)单调递增,因0<m<n<1,所以h(m)<h(n),从而有
>0,于是h(x)在(0,1)单调递增,因0<m<n<1,所以h(m)<h(n),从而有![]() ,再设φ(x)=
,再设φ(x)=![]() ,x>0 ,通过导数来验证φ(x)增减性,进一步通过增减性求得最值,即可求证不等式成立
,x>0 ,通过导数来验证φ(x)增减性,进一步通过增减性求得最值,即可求证不等式成立
解:(1)①当![]() 时, g(x)=xlnx-x+|x+
时, g(x)=xlnx-x+|x+![]() |=xlnx+
|=xlnx+![]() ,
,
g′(x)=1+lnx,
当0<x<![]() 时,g′(x)<0;当x>
时,g′(x)<0;当x>![]() 时,g′(x)>0;
时,g′(x)>0;
因此g(x)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增,
,+∞)上单调递增,
又![]() ,g(
,g(![]() )=-
)=-![]() +
+![]() <0,g(1)=
<0,g(1)=![]() >0,
>0,
所以g(x)有且仅有两个零点.
②(i)当a≤![]() 时,g (x)=xlnx-x+x-a=xlnx-a,
时,g (x)=xlnx-x+x-a=xlnx-a,
因为x∈[![]() ,e],g′(x)=1+lnx≥0恒成立,
,e],g′(x)=1+lnx≥0恒成立,
所以g(x)在[![]() ,e]上单调递增,所以此时g(x)的最小值为g(
,e]上单调递增,所以此时g(x)的最小值为g(![]() )=-
)=-![]() -a.
-a.
(ii)当a≥e时,g(x)=xlnx-x+a-x=xlnx-2x+a,
因为x∈[![]() ,e],g′(x)=lnx-1≤0恒成立,
,e],g′(x)=lnx-1≤0恒成立,
所以g(x)在[![]() ,e]上单调递减,所以此时g(x)的最小值为g(e)=a-e.
,e]上单调递减,所以此时g(x)的最小值为g(e)=a-e.
(iii)当![]() <a<e时,
<a<e时,
若![]() ≤x≤a,则g(x)=xlnx-x+a-x=xlnx-2x+a,
≤x≤a,则g(x)=xlnx-x+a-x=xlnx-2x+a,
若a≤x≤e,则g(x)=xlnx-x+x-a=xlnx-a,
由(i),(ii)知g(x)在[![]() ,a]上单调递减,在[a,e]上单调递增,
,a]上单调递减,在[a,e]上单调递增,
所以此时g(x)的最小值为g(a)=alna-a,
综上有:当a≤![]() 时,g(x)的最小值为-
时,g(x)的最小值为-![]() -a;
-a;
当![]() <a<e时,g(x)的最小值为alna-a;
<a<e时,g(x)的最小值为alna-a;
当a≥e时,g(x)的最小值为a-e.
(2)设h(x)=![]() ,
,
则当x∈(0,1)时,h′(x)= >0,于是h(x)在(0,1)单调递增,
>0,于是h(x)在(0,1)单调递增,
又0<m<n<1,所以h(m)<h(n),
从而有![]()
设φ(x)=![]() ,x>0
,x>0
则φ′(x)=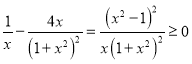
因此φ(x)在(0,+∞)上单调递增,
因为0<n<1,所以φ(n)<φ(1)=0,即lnn-1+![]() <0,
<0,
因此![]()
即原不等式得证.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(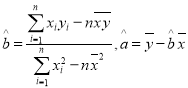 )
)
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 的正半轴建立平面直角坐标系
的正半轴建立平面直角坐标系![]() .
.
(1)求![]() 和
和![]() 的参数方程;
的参数方程;
(2)已知射线![]() ,将
,将![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,且
,且![]() 与
与![]() 交于
交于![]() 两点,
两点, ![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 取得最大值时点
取得最大值时点![]() 的极坐标.
的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=1,PA=AB=![]() ,点E是棱PB的中点.
,点E是棱PB的中点.

(1)求异面直线EC与PD所成角的余弦值;
(2)求二面角B-EC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队,平均分到甲、乙两个村进行义务巡诊,其中每个分队都必须有内科医生、外科医生和护士,则不同的分配方案有
A. 72种 B. 36种 C. 24种 D. 18种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别是椭圆的左、右焦点,直线
分别是椭圆的左、右焦点,直线![]() 过点
过点![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() 使
使![]() 的面积为
的面积为![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为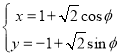 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() ,求
,求![]() 的最大值及此时直线
的最大值及此时直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com