
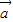 =(sinx,
=(sinx,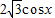 ),
),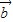 =(2sinx,sinx),设
=(2sinx,sinx),设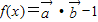 ,
, ,求f(x)的值域;
,求f(x)的值域;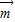 =(t,0)作长度最短的平移后,其图象关于原点对称,求
=(t,0)作长度最短的平移后,其图象关于原点对称,求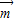 的坐标.
的坐标.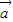 =(sinx,
=(sinx,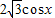 ),
),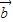 =(2sinx,sinx),设
=(2sinx,sinx),设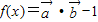 ,根据向量数量积计算公式,我们易求出f(x)的解析式,利用降幂公式(二倍角公式逆用)及辅助角公式,我们可将其化为正弦型函数的形式,进而根据正弦型函数的图象和性质,得到(x)的最小正周期及单调递增区间;
,根据向量数量积计算公式,我们易求出f(x)的解析式,利用降幂公式(二倍角公式逆用)及辅助角公式,我们可将其化为正弦型函数的形式,进而根据正弦型函数的图象和性质,得到(x)的最小正周期及单调递增区间;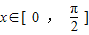 及正弦型函数的图象和性质,可求出此时f(x)的值域;
及正弦型函数的图象和性质,可求出此时f(x)的值域;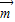 =(t,0)作长度最短的平移后,其图象关于原点对称,即此时原点是f(x)的对称中心,根据(1)中解析式,求出函数f(x)的距离原点最近的对称中心,即可得到
=(t,0)作长度最短的平移后,其图象关于原点对称,即此时原点是f(x)的对称中心,根据(1)中解析式,求出函数f(x)的距离原点最近的对称中心,即可得到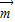 的坐标.
的坐标. =
=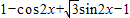 =
=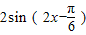 (4分)
(4分)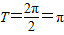
 (k∈Z)
(k∈Z)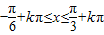 (k∈Z)
(k∈Z)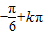 ,
,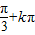 ](k∈Z)(7分)
](k∈Z)(7分)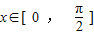 ∴
∴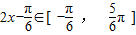
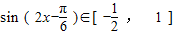 ∴f(x)∈[-1,2](10分)
∴f(x)∈[-1,2](10分)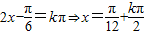 (k∈Z)
(k∈Z)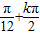 ,0)(k∈Z)
,0)(k∈Z)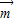 的长度最短的平移
的长度最短的平移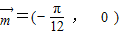 (13分)
(13分)

科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| 2 |
| b |
| a |
| b |
| a |
| b |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| b |
| a |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com