练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．在平行六面体ABCD-A1B1C1D1中，化简$\overrightarrow{AB}+\overrightarrow{C{C_1}}-\overrightarrow{DB}$为（　　）
    A．$\overrightarrow{A{C}_{1}}$B．$\overrightarrow{C{A}_{1}}$C．$\overrightarrow{A{D_1}}$D．$\overrightarrow{{D_1}A}$

    分析 由平行六边体的性质得$\overrightarrow{AB}+\overrightarrow{C{C_1}}-\overrightarrow{DB}$=$\overrightarrow{AB}+\overrightarrow{B{B}_{1}}+\overrightarrow{{B}_{1}{D}_{1}}$，由此能求出结果．

    解答 解：如图，在平行六面体ABCD-A1B1C1D1中，
    $\overrightarrow{AB}+\overrightarrow{C{C_1}}-\overrightarrow{DB}$=$\overrightarrow{AB}+\overrightarrow{B{B}_{1}}+\overrightarrow{{B}_{1}{D}_{1}}$=$\overrightarrow{A{D}_{1}}$．
    故选：C．

    点评 本题考查向量求和，是基础题，解题时要认真审题，注意空间向量加法法则的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    19．已知f（x）是定义在R上的奇函数，当x＞0时，f（x）=x2-4x，则不等式f（x）＞x的解集为（-5，0）∪（5，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知α∈（0，π），$cosα=-\frac{1}{2}$，则sin2α=（　　）
    A．$±\frac{{\sqrt{3}}}{2}$B．$±\frac{1}{2}$C．$-\frac{{\sqrt{3}}}{2}$D．$-\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知函数f（x）=（x2+x-1）ex，则f（x）的极大值为$\frac{5}{{e}^{3}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设a，b∈R，函数f（x）=ax+b（0≤x≤1），则f（x）＞0恒成立是a+2b＞0成立的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．即不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．设数列{an}满足条件a1=1，an+1=an+3•2n-1．
    （1）求数列{an}的通项公式；
    （2）若$\frac{b_n}{a_n}$=n，求数列{bn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

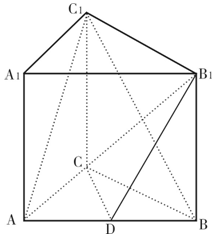    1．如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=3，BC=4，AB=5，点D是AB的中点．
    （1）求证AC⊥BC1
    （2）求证AC1∥平面CDB1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

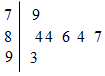    18．如图是2013年中央电视台举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（　　）
    A．85，1.6B．84，4C．84，1.6D．85，4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在下列条件下，分别求出有多少种不同的做法？
    （1）5个不同的球，放入4个不同的盒子，每盒至少一球；
    （2）5个相同的球，放入4个不同的盒子，每盒至少一球．

    查看答案和解析>>

    同步练习册答案