
 ,
, ,
, ,
, ,
,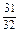 ,…;
,…; ,-
,- ,
, ,-
,- ,
, ,…;
,…; ,-1,
,-1,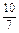 ,-
,- ,
, ,-
,- ,…;
,…; .(3)an=(-1)n·
.(3)an=(-1)n· .也可写为an=
.也可写为an= .
. .(5)an=
.(5)an= (10n-1).
(10n-1). .
. .
. .
. ,-
,- ,
, .
. ,
, ,
, ,
, ,…,分母都是3,而分子分别是10-1,102-1,103-1,104-1,…,
,…,分母都是3,而分子分别是10-1,102-1,103-1,104-1,…, (10n-1).
(10n-1).

 智能训练练测考系列答案
智能训练练测考系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com