
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的焦点且垂直于
的焦点且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 均在椭圆
均在椭圆![]() 上,点
上,点![]() 在抛物线
在抛物线![]() 上,若
上,若![]() 的重心为坐标原点
的重心为坐标原点![]() ,且
,且![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
科目:高中数学 来源: 题型:
【题目】已知椭圆方程为![]() ,左,右焦点分别为
,左,右焦点分别为![]() ,上顶点为A,
,上顶点为A,![]() 是面积为4的直角三角形.
是面积为4的直角三角形.
(1)求椭圆的标准方程;
(2)过![]() 作直线与椭圆交于P,Q两点,求
作直线与椭圆交于P,Q两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果方程![]() y|y|=1所对应的曲线与函数y=f(x)的图象完全重合,那么对于函数y=f(x)有如下结论:
y|y|=1所对应的曲线与函数y=f(x)的图象完全重合,那么对于函数y=f(x)有如下结论:
①函数f(x)在R上单调递减;
②y=f(x)的图象上的点到坐标原点距离的最小值为1;
③函数f(x)的值域为(﹣∞,2];
④函数F(x)=f(x)+x有且只有一个零点.
其中正确结论的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 绕直线
绕直线![]() 翻转成
翻转成![]() (
(![]() 平面
平面![]() ),
),![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中,①与平面
翻折过程中,①与平面![]() 垂直的直线必与直线
垂直的直线必与直线![]() 垂直;②线段
垂直;②线段![]() 的长恒为
的长恒为![]() ③异面直线
③异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ④当三棱锥的体积最大时,三棱锥
④当三棱锥的体积最大时,三棱锥![]() 外接球的体积是
外接球的体积是![]() .上面说法正确的所有序号是( )
.上面说法正确的所有序号是( )
A.①②④B.①③④C.②③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,过点P(1,2)的直线l的参数方程为 为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的AQI指数M与当天的空气水平可见度y(单位:cm)的情况如下表:
M | 900 | 700 | 300 | 100 |
y | 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2019年12月份AQI指数M的频数分布表如下:
M |
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,若x与y之间具有线性关系,试根据上述数据求出y关于x的线性回归方程;
,若x与y之间具有线性关系,试根据上述数据求出y关于x的线性回归方程;
(2)王先生在该市开了一家洗车店,洗车店每天的平均收入与AQI指数的相关关系如下表:
M |
|
|
|
|
|
日均收入(元) | -2000 | -1000 | 2000 | 6000 | 8000 |
估计王先生的洗车店2019年12月份每天的平均收入.
附参考公式:![]() ,其中
,其中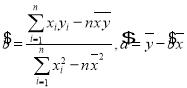
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() 的左右焦点分别为的
的左右焦点分别为的![]() 、
、![]() ,离心率为
,离心率为![]() ;过抛物线
;过抛物线![]() 焦点
焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,当
两点,当![]() 时,
时, ![]() 点在
点在![]() 轴上的射影为
轴上的射影为![]() 。连结
。连结![]() 并延长分别交
并延长分别交![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ;
; ![]() 与
与![]() 的面积分别记为
的面积分别记为![]() ,
, ![]() ,设
,设![]() .
.
(Ⅰ)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(Ⅱ)求![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com