
����������14�֣�
�м��������༶������ѧ�� �ԣ����մ��ڵ���85��Ϊ���㣬85������Ϊ������ͳ�Ƴɼ��õ����µ�������.
�ԣ����մ��ڵ���85��Ϊ���㣬85������Ϊ������ͳ�Ƴɼ��õ����µ�������.
| | ���� | ������ | �ܼ� |
| �װ� | 10 | | |
| �Ұ� | | 30 | |
| �ϼ� | | | 105 |
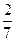
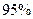 �Ŀɿ���Ҫ���ܷ���Ϊ���ɼ���༶�й�ϵ��.
�Ŀɿ���Ҫ���ܷ���Ϊ���ɼ���༶�й�ϵ��. ��.
��.
�⣺�����������е����ݣ��õ� ��������������5��
��������������5��
�����95%�İ�����Ϊ���ɼ���༶�й�ϵ����������������7��
(�� )��������ķ����Ӽװ������ѧ����ȡһ�ˣ��Ѽװ������10��ѧ����2��11���б�ţ��Ⱥ���������һö���ȵ����ӣ����ֵĵ���֮��Ϊ����ȡ�˵����.����鵽6��10�ŵĸ���.
)��������ķ����Ӽװ������ѧ����ȡһ�ˣ��Ѽװ������10��ѧ����2��11���б�ţ��Ⱥ���������һö���ȵ����ӣ����ֵĵ���֮��Ϊ����ȡ�˵����.����鵽6��10�ŵĸ���.
�⣺�衰�鵽6��10�š�Ϊ�¼�A���Ⱥ���������һö���ȵ����ӣ����ֵĵ���Ϊ��x��y����������������8��
���еĻ����¼��У�1��1������1��2������1��3����������6��6����
��36������������������10��
�¼�A�����Ļ����¼��У�
��1��5������2��4������3��3������4��2������5��1����4��6������5��5������6��4������8����������12��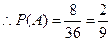 ��������������14��
��������������14��
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����������14�֣�
 ����������С��,�ֱ�λ��
����������С��,�ֱ�λ��![]() ���㴦����
���㴦����![]() ��
��![]() . ��ƻ��Ͻ�һ�����վ��Ϊͬʱ��������С����������
. ��ƻ��Ͻ�һ�����վ��Ϊͬʱ��������С����������![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����
�ϵ�![]() �㴦����������ϵ��ͼ����
�㴦����������ϵ��ͼ����![]() .
.
(��) ��ϣ�����վ![]() ������С���ľ������С��
������С���ľ������С��
��![]() Ӧλ�ںδ���
Ӧλ�ںδ���
(��) ��ϣ����![]() ������С������Զ����Ϊ��С��
������С������Զ����Ϊ��С��
��![]() Ӧλ�ںδ���
Ӧλ�ںδ���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
(��������14��)
 ij�������ҹ������ֱ�λ�ھ���ABCD�Ķ���A��B��CD���е�P������֪AB=20km��BC=10km��Ϊ�˴������ҹ�������ˮ����Ҫ�ھ���ABCD�������ϣ����߽磩����A��B��Ⱦ����һ��O������һ����ˮ�����������������۹ܵ�AO��BO��OP�������۹ܵ����ܳ�Ϊykm��
ij�������ҹ������ֱ�λ�ھ���ABCD�Ķ���A��B��CD���е�P������֪AB=20km��BC=10km��Ϊ�˴������ҹ�������ˮ����Ҫ�ھ���ABCD�������ϣ����߽磩����A��B��Ⱦ����һ��O������һ����ˮ�����������������۹ܵ�AO��BO��OP�������۹ܵ����ܳ�Ϊykm��
��1��������Ҫ��д��������ϵʽ��
�����BAO=��(rad)����y��ʾ�ɦȵĺ�����ϵʽ��
����OP=x(km)����y��ʾ��x�ĺ�����ϵʽ��
��2������ѡ�ã�1���е�һ��������ϵʽ��ȷ����ˮ��������λ�ã�ʹ�������۹ܵ��ܳ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
(��������14��)
 ij�������ҹ������ֱ�λ�ھ���ABCD�Ķ���A��B��CD���е�P������֪AB=20km��BC=10km��Ϊ�˴������ҹ�������ˮ����Ҫ�ھ���ABCD�������ϣ����߽磩����A��B��Ⱦ����һ��O������һ����ˮ�����������������۹ܵ�AO��BO��OP�������۹ܵ����ܳ�Ϊykm��
ij�������ҹ������ֱ�λ�ھ���ABCD�Ķ���A��B��CD���е�P������֪AB=20km��BC=10km��Ϊ�˴������ҹ�������ˮ����Ҫ�ھ���ABCD�������ϣ����߽磩����A��B��Ⱦ����һ��O������һ����ˮ�����������������۹ܵ�AO��BO��OP�������۹ܵ����ܳ�Ϊykm��
��1��������Ҫ��д��������ϵʽ��
�����BAO=��(rad)����y��ʾ�ɦȵĺ�����ϵʽ��
����OP=x(km)����y��ʾ��x�ĺ�����ϵʽ��
��2������ѡ�ã�1���е�һ��������ϵʽ��ȷ����ˮ��������λ�ã�ʹ�������۹ܵ��ܳ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010-2011ѧ��㶫ʡ����ȫ��ģ�⿼����ѧ�ľ� ���ͣ������
����������14�֣�
�м��������༶������ѧ���ԣ����մ��ڵ���85��Ϊ���㣬85������Ϊ������ͳ�Ƴɼ��õ����µ�������.
|
|
���� |
������ |
�ܼ� |
|
�װ� |
10 |
|
|
|
�Ұ� |
|
30 |
|
|
�ϼ� |
|
|
105 |
��֪��ȫ��105���г鵽�����ȡ1��Ϊ����ĸ���Ϊ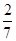
(��)������������������
(��)���������������ݣ����� �Ŀɿ���Ҫ���ܷ���Ϊ���ɼ���༶�й�ϵ�� .
�Ŀɿ���Ҫ���ܷ���Ϊ���ɼ���༶�й�ϵ�� .
(��)��������ķ����Ӽװ������ѧ����ȡһ�ˣ��Ѽװ������10��ѧ����2��11���б�ţ��Ⱥ���������һö���ȵ����ӣ����ֵĵ���֮��Ϊ����ȡ�˵����.����鵽6��10�ŵĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010��㶫ʡ�߶���ѧ�ڵ�һ�ζο�������ѧ�� ���ͣ������
(��������14��)����һ��߳�Ϊ4�������θְ壬�ֶ����и���ӳ�һ����������������(�С�����ĺ��Բ���)������Ӧ����ѧ֪ʶ��������ƣ��ڸְ���ĸ��Ǵ�����ȥһ���߳�Ϊ
 ��С�����Σ����ಿ��Χ��һ�������壬�ó�����ĸ���С�����εı߳���
��С�����Σ����ಿ��Χ��һ�������壬�ó�����ĸ���С�����εı߳���
(1)������������и���Ӷ��ɵij����������ĵ��ݻ�V1���� ��ʾ����
��ʾ����
(2)������ƣ�1���ķ���������õ��� ʱ��Vlȡ���ֵ
ʱ��Vlȡ���ֵ ��Ϊ�˲����˷����٣�����ʦ����ʵ�������������ӷ�������д���루1���ĺ��ӷ������ѣ�ʹ�����˷����٣��ݻ���Vl����Ʒ��������������������Ʒ������õ����������ݻ���
��Ϊ�˲����˷����٣�����ʦ����ʵ�������������ӷ�������д���루1���ĺ��ӷ������ѣ�ʹ�����˷����٣��ݻ���Vl����Ʒ��������������������Ʒ������õ����������ݻ���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com