
 满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数 使得
使得 成立,记这样的
成立,记这样的 的个数为
的个数为 ,则得到一个新数列
,则得到一个新数列 。例如,若数列
。例如,若数列 是1,2,3,……,
是1,2,3,……, ,…,则数列
,…,则数列 是0,1,2,…,
是0,1,2,…, , ….已知对任意的
, ….已知对任意的 ,
, ,则
,则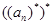 = 。
= 。 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 ,
,

 并猜测
并猜测 的表达式;
的表达式; +
+ +
+ +…+
+…+
 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,第2个五角形数记作
,第2个五角形数记作 ,第3个五角形数记作
,第3个五角形数记作 ,第4个五角形数记作
,第4个五角形数记作 ,……,若按此规律继续下去,则
,……,若按此规律继续下去,则 ,若
,若 ,则
,则 .
.
 1 5 12 22
1 5 12 22
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,内切圆的半径为
,内切圆的半径为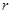 ,则三角形的面积为
,则三角形的面积为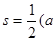
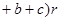 ;四面体的四个面的面积分别为
;四面体的四个面的面积分别为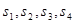 ,内切球的半径为
,内切球的半径为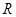 .类比三角形的面积可得四面体的体积为( )
.类比三角形的面积可得四面体的体积为( )A. | B. |
C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com