练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    判断下列复合命题的真假:

    （1）面积相等或周长相等的圆是等圆；

    （2）任何集合都不是空集的子集；

    （3）一个有理数与一个无理数的和、积都是无理数.

    思路解析：先分析判断复合命题的构成形式，再分别判断每个命题的真假，利用真值表进行判断.

    解：（1）真命题.因为p：“面积相等的圆是等圆”，q：“周长相等的圆是等圆”都是真命题，所以命题（1）p或q是真命题.

    （2）假命题.可通过反例说明它是假命题.

    （3）假命题.因为p：“一个有理数与一个无理数的和是无理数”是真命题，

    q：“一个有理数与一个无理数的积是无理数”是假命题（反例0·2=0），所以命题（3）p且q是假命题.

    方法点拨

    判断一个简单命题的真假时，真命题需作一定的推理论证，而假命题只需作一个反例说明不真即可；判断复合命题的真假，先转化成判断简单命题的真假，再利用真值表作出对复合命题真假的判断.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    1、由“p：8+7=16，q：π＞3”构成的复合命题，下列判断正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    由命题p：“函数y=
    1
    2
    (ex-e-x)     是奇函数”，与q：“数列a，a2，a3，…，a n，…是等比数列”构成的复合命题中，下列判断正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列各组命题：
    （1）p：15是5的倍数，q：15是3的倍数；
    （2）p：?m∈R，|m|＞0，q：?a∈R，a2＞2；
    （3）p：?α∈R，sinα＞1，q：?θ∈R，cosθ＜1．
    判断由各组命题构成的“p∨q“、“p∧q“、“?p”形式的复合命题的真假，并把相应的判断结果（“真’’或“假”）填在下列表格中：
    题号  p∨q  p∧q ￢p 
    （1）      
    （2）      
    （3）      

    查看答案和解析>>

    科目：高中数学 来源：新教案 高一数学 题型：008

    指出下列复合命题的构成形式及构成它的简单命题，判断复合命题的真假，并说明真假的理由；

    (1)(n－1)·n·(n＋1)(n∈N*)既能被2整除，也能被3整除；

    (   )

    (2)5≥3；

    (   )

    (3)正方形不是菱形；

    (   )

    (4)是{}的元素，也是{}的真子集．

    (   )

    查看答案和解析>>

    科目：高中数学 来源：黄冈重点作业·高三数学（下） 题型：008

    判断下列复合命题的真假：

    (1)方程x2＋3x＋2＝0的根是x＝±1．

    (   )

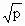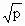    (2)在所有正实数中，是正数，且＜p．

    (   )

    (3)空集不是集合{}的真子集．

    (   )

    查看答案和解析>>

    同步练习册答案