
【题目】设椭圆![]() (
(![]() )的左、右焦点为
)的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .已知
.已知![]() .
.
(1)求椭圆的离心率;
(2)设![]() 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,经过原点
,经过原点![]() 的直线
的直线![]() 与该圆相切,求直线
与该圆相切,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 的斜率为
的斜率为![]() 或
或![]() .
.
【解析】试题(1)设椭圆的右焦点![]() 的坐标为
的坐标为![]() ,由已知
,由已知![]() ,可得
,可得![]() ,结合
,结合![]() ,可得
,可得![]() ,从而可求得椭圆的离心率;(2)在(1)的基础上,可先利用
,从而可求得椭圆的离心率;(2)在(1)的基础上,可先利用![]() 及数量积的坐标运算求出
及数量积的坐标运算求出![]() 点的坐标,再求出以线段
点的坐标,再求出以线段![]() 为直径的圆的方程(圆心坐标和半径),最后设经过原点
为直径的圆的方程(圆心坐标和半径),最后设经过原点![]() 的与该圆相切的直线
的与该圆相切的直线![]() 的方程为
的方程为![]() ,由圆心到切线的距离等于半径,列方程,解方程即可得求得直线
,由圆心到切线的距离等于半径,列方程,解方程即可得求得直线![]() 的斜率.
的斜率.
(1)设椭圆的右焦点![]() 的坐标为
的坐标为![]() .由
.由![]() ,可得
,可得![]() ,又
,又![]() ,则
,则![]() ,∴椭圆的离心率
,∴椭圆的离心率![]() .
.
(2)由(1)知![]() ,
, ![]() ,故椭圆方程为
,故椭圆方程为![]() .设
.设![]() .由
.由![]() ,
, ![]() ,有
,有![]() ,
, ![]() .由已知,有
.由已知,有![]() ,即
,即![]() .又
.又![]() ,故有
,故有![]() ①
①
又∵点![]() 在椭圆上,故
在椭圆上,故![]() ②
②
由①和②可得![]() .而点
.而点![]() 不是椭圆的顶点,故
不是椭圆的顶点,故![]() ,代入①得
,代入①得![]() ,即点
,即点![]() 的坐标为
的坐标为![]() .设圆的圆心为
.设圆的圆心为![]() ,则
,则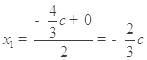 ,
,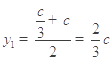 ,进而圆的半径
,进而圆的半径![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() ,依题意,直线
,依题意,直线![]() 的方程为
的方程为![]() .由
.由![]() 与圆相切,可得
与圆相切,可得![]() ,即
,即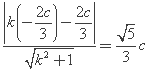 ,整理得
,整理得![]() ,解得
,解得![]() .∴直线
.∴直线![]() 的斜率为
的斜率为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】将边长为![]() 的正方形
的正方形![]() 沿对角线
沿对角线![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,在折起后形成的三棱锥
,在折起后形成的三棱锥![]() 中,给出下列四个命题:①
中,给出下列四个命题:①![]() ;②异面直线
;②异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;③二面角
;③二面角![]() 余弦值为
余弦值为![]() ;④三棱锥
;④三棱锥![]() 的体积是
的体积是![]() .其中正确命题的序号是___________.(写出所有正确命题的序号)
.其中正确命题的序号是___________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,求三条曲线
,求三条曲线![]() ,
,![]() ,
,![]() 所围成图形的面积.
所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组测量电视塔AE的高度H(单位m),如示意图,垂直放置的标杆BC高度h=4m,仰角∠ABE=α,∠ADE=β

(1)该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,,请据此算出H的值
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m,问d为多少时,α-β最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知矩形![]() 所在平面与半圆弧
所在平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是半圆弧
是半圆弧![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
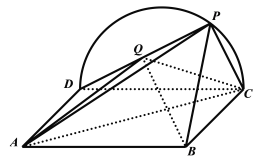
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,当三棱锥
,当三棱锥![]() 的体积最大且二面角
的体积最大且二面角![]() 的平面角的大小为
的平面角的大小为![]() 时,试确定
时,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,M是椭圆C的上顶点,
,M是椭圆C的上顶点,![]() ,F2是椭圆C的焦点,
,F2是椭圆C的焦点,![]() 的周长是6.
的周长是6.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过动点P(1,t)作直线交椭圆C于A,B两点,且|PA|=|PB|,过P作直线l,使l与直线AB垂直,证明:直线l恒过定点,并求此定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为2个单位)的顶点
(边长为2个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走了几个单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走了几个单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到起点
个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到起点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )
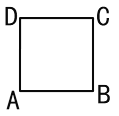
A.21种B.22种C.25种D.27种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com