
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 是曲线
是曲线![]() :
:![]() 上的动点,将
上的动点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,点![]() ,射线
,射线![]() 与曲线
与曲线![]() ,
,![]() 分别相交于异于极点
分别相交于异于极点![]() 的
的![]() 两点,求
两点,求![]() 的面积.
的面积.
【答案】(1)曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]() ;(2)
;(2)![]()
【解析】
(1)由题意,点Q的轨迹是以(2,0)为圆心,以2为半径的圆,写出其普通方程,再结合ρ2=x2+y2,x=ρcosθ,y=ρsinθ,可得曲线C1,C2的极坐标方程;
(2)在极坐标系中,设A,B的极径分别为ρ1,ρ2,求得|AB|=|ρ1﹣ρ2|,再求出M(3,![]() )到射线
)到射线![]() 的距离h=
的距离h=![]() ,即可求得△MAB的面积.
,即可求得△MAB的面积.
(1)由题意,点Q的轨迹是以(2,0)为圆心,以2为半径的圆,则曲线C2:![]() ,
,
∵ρ2=x2+y2,x=ρcosθ,y=ρsinθ,∴曲线C1的极坐标方程为ρ=4sinθ,曲线C2的极坐标方程为ρ=4cosθ;
(2)在极坐标系中,设A,B的极径分别为ρ1,ρ2,![]()
又![]() 点
点![]() 到射线
到射线![]() 的距离为
的距离为![]()
![]() 的面积
的面积![]()


科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处取得极值A,函数
处取得极值A,函数![]() ,其中
,其中![]() …是自然对数的底数.
…是自然对数的底数.
(1)求m的值,并判断A是![]() 的最大值还是最小值;
的最大值还是最小值;
(2)求![]() 的单调区间;
的单调区间;
(3)证明:对于任意正整数n,不等式![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆![]() ,圆心
,圆心![]() ,点E在直线
,点E在直线![]() 上,点P满足
上,点P满足![]() ,
,![]() ,点P的轨迹为曲线M.
,点P的轨迹为曲线M.
(1)求曲线M的方程.
(2)过点N的直线l分别交M于点A、B,交圆N于点C、D(自上而下),若![]() 、
、![]() 、
、![]() 成等差数列,求直线l的方程.
成等差数列,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情期间,一同学通过网络平台听网课,在家坚持学习.某天上午安排了四节网课,分别是数学,语文,政治,地理,下午安排了三节,分别是英语,历史,体育.现在,他准备在上午下午的课程中各任选一节进行打卡,则选中的两节课中至少有一节文综学科(政治、历史、地理)课程的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案规定,普通高中学业水平考试分为合格性考试(合格考)和选择性考试(选择考).其中“选择考”成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原始卷面分数,由高到低进行排序,评定为A,B,C,D,E五个等级.某试点高中2019年参加“选择考”总人数是2017年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2017年和2019年“选择考”成绩等级结果,得到如图表:
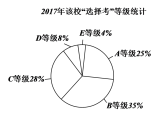

针对该校“选择考”情况,2019年与2017年比较,下列说法正确的是( )
A.获得A等级的人数不变B.获得B等级的人数增加了1倍
C.获得C等级的人数减少了D.获得E等级的人数不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,![]() ,
,![]()

(Ⅰ)证明;AC⊥BP;
(Ⅱ)求直线AD与平面APC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com