
分析 (1)由题意可知::|EM|+|EC|=|EN|+|EC|=|NC|=4,故动点E的轨迹为以M,C为焦点,长轴为4的椭圆,分别求得a、b和c的值,求得动点E的轨迹方程C1;
(2)设出直线l的方程,代入椭圆方程,由韦达定理求得x1+x2及x1x2,利用导数法求得直线PA和PB的斜率,由PA⊥PB,求得m的值,直线l过抛物线C2的焦点F,求得交点S的坐标,根据点到直线的距离公式,求得S到到直线l:kx-y+1=0的距离d,根据弦长公式求得丨PQ丨及|AB|,由$d=\sqrt{|{AB}|•|{PQ}|}$,求得28k4+36k2+7=0,此方程无解,不存在直线l,使得 $d=\sqrt{|{AB}|•|{PQ}|}$.
解答 解:(1)依题意有:|EM|+|EC|=|EN|+|EC|=|NC|=4,故动点E的轨迹为以M,C为焦点,长轴为4的椭圆.
于是:$a=2,c=\sqrt{2}$,从而$b=\sqrt{2}$,故动点E的轨迹方程C1为:$\frac{x^2}{4}+\frac{y^2}{2}=1$.
(2)设直线l:y=kx+m,A(x1,y1),B(x2,y2),P(x3,y3)Q(x4,y4),由$\left\{\begin{array}{l}y=kx+m\\{x^2}=4y\end{array}\right.$,
得:x2-4kx-4m=0,故x1+x2=4k,x1x2=-4m.
由x2=4y得:$y=\frac{1}{4}{x^2}$,即切线斜率$k=y'=\frac{x}{2}$.
于是:${k_{PA}}=\frac{x_1}{2},{k_{PB}}=\frac{x_2}{2}$,
由PA⊥PB得;${k_{PA}}•{k_{PB}}=\frac{x_1}{2}×\frac{x_2}{2}=\frac{{{x_1}{x_2}}}{4}=-m=-1$,
解得:m=1,
这说明直线l过抛物线C2的焦点F,由$\left\{\begin{array}{l}y=\frac{x_1}{2}x-\frac{x_1^2}{4}\\ y=\frac{x_2}{2}x-\frac{x_2^2}{4}\end{array}\right.$,
得:$x=\frac{{{x_1}+{x_2}}}{2}=2k,y=\frac{x_1}{2}•2k-\frac{x_1^2}{4}=k{x_1}-\frac{x_1^2}{4}=\frac{{{x_1}+{x_2}}}{2}{x_1}-\frac{x_1^2}{4}=\frac{{{x_1}{x_2}}}{4}=-1$即S(2k,-1).
于是:点S(2k,-1)到直线l:kx-y+1=0的距离$d=\frac{{2{k^2}+2}}{{\sqrt{1+{k^2}}}}=2\sqrt{1+{k^2}}$,
由$\left\{\begin{array}{l}y=kx+1\\{x^2}+2{y^2}=4\end{array}\right.$得:(1+2k2)x2+4kx-2=0,
从而$|{PQ}|=\sqrt{1+{k^2}}\frac{{\sqrt{{{({4k})}^2}-4({1+2{k^2}})•({-2})}}}{{1+2{k^2}}}=\sqrt{1+{k^2}}\frac{{\sqrt{8({1+4{k^2}})}}}{{1+2{k^2}}}$,
同理:|AB|=4(1+k2),
由$d=\sqrt{|{AB}|•|{PQ}|}$得$2\sqrt{({1+2{k^2}})}=\sqrt{4({1+{k^2}})•({1+{k^2}})\frac{{\sqrt{8({1+4{k^2}})}}}{{1+2{k^2}}}}$,
化简整理,得:28k4+36k2+7=0,此方程无解,
所以不存在直线l,使得 $d=\sqrt{|{AB}|•|{PQ}|}$.
点评 本题考查椭圆的轨迹方程,考查直线与椭圆的位置关系,一元二次方程根与系数的关系,点到直线的距离公式等知识的综合运用,考查分析问题及解决问题的能力,属于中档题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0<c | B. | x0>c | C. | x0<b | D. | x0>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
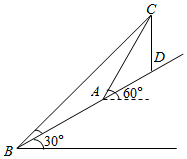 如图,要在山坡上A、B两处测量与地面垂直的铁塔CD的高,由A、B两处测得塔顶C的仰角分别为60°和45°,AB长为40m,斜坡与水平面成30°角,则铁塔CD的高为$\frac{40\sqrt{3}}{3}$m.
如图,要在山坡上A、B两处测量与地面垂直的铁塔CD的高,由A、B两处测得塔顶C的仰角分别为60°和45°,AB长为40m,斜坡与水平面成30°角,则铁塔CD的高为$\frac{40\sqrt{3}}{3}$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
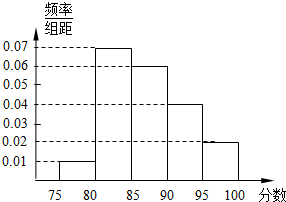 有某单位在2016年的招聘考试中100名竞聘者的笔试成绩,按成绩分组为:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
有某单位在2016年的招聘考试中100名竞聘者的笔试成绩,按成绩分组为:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com