
【题目】对于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.![]() 在
在![]() 处取得极大值
处取得极大值![]()
B.![]() 有两个不同的零点
有两个不同的零点
C.![]()
D.若![]() 在
在![]() 恒成立,则
恒成立,则![]()
【答案】ACD
【解析】
对选项A,求出函数的单调区间,再求出极大值即可判断A正确,对选项B,利用函数的单调性和最值即可判断B错误,对选项C,首先利用函数的单调性即可得到![]() ,再构造函数
,再构造函数![]() ,利用
,利用![]() 的单调性即可得到
的单调性即可得到![]() ,最后即可判断C正确,对选项D,转化为
,最后即可判断C正确,对选项D,转化为![]() 在在
在在![]() 恒成立,构造函数
恒成立,构造函数![]() ,求出最大值即可判断D正确.
,求出最大值即可判断D正确.
对选项A,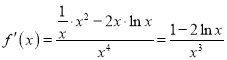 ,
,![]() .
.
令![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() 为增函数,
为增函数,
![]() ,
,![]() ,
,![]() 为减函数.
为减函数.
所以![]() 处取得极大值
处取得极大值![]() ,故A正确.
,故A正确.
对选项B,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,又因为
,又因为![]() ,
,
所以![]() 只有一个零点,故B错误.
只有一个零点,故B错误.
对选项C,因为![]() 在区间
在区间![]() 单调递减,且
单调递减,且![]() ,
,
所以![]() .
.
![]() ,
,![]() .
.
设![]() ,
,![]() .
.
令![]() ,
,![]() .
.
所以![]() 时,
时,![]() ,
,![]() 为减函数.
为减函数.
又因为![]() ,所以
,所以![]() ,
,![]() .
.
即![]() ,所以
,所以![]() ,故C正确.
,故C正确.
对选项D,![]() 在在
在在![]() 恒成立.
恒成立.
设![]() ,
,![]() ,令
,令![]() ,
,![]() .
.
当![]() ,
,![]() ,
,![]() 为增函数,
为增函数,
当![]() ,
,![]() ,
,![]() 为减函数.
为减函数.
所以![]() ,即
,即![]() ,故D正确.
,故D正确.
故答案为:ACD


科目:高中数学 来源: 题型:
【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 |
|
|
|
|
|
管理时间 |
|
|
|
|
|
并调查了某村![]() 名村民参与管理的意愿,得到的部分数据如下表所示:
名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 |
|
|
女性村民 |
|
![]() 求出相关系数
求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
![]() 若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取
若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取![]() 人,记取到不愿意参与管理的男性村民的人数为
人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
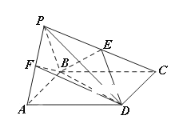
【题目】如图,四棱锥![]() 中,
中,![]() 是正三角形,四边形ABCD是矩形,且平面
是正三角形,四边形ABCD是矩形,且平面![]() 平面
平面![]() .
.
(1)若点E是PC的中点,求证:![]() 平面BDE;
平面BDE;
(2)若点F在线段PA上,且![]() ,当三棱锥
,当三棱锥![]() 的体积为
的体积为![]() 时,求实数
时,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的非负半轴重合,若曲线
轴的非负半轴重合,若曲线![]() 的极坐标系方程为
的极坐标系方程为
![]() ,直线
,直线![]() 的参数方程为
的参数方程为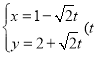 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(2)设点![]() 直线
直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点, 求
两点, 求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com