
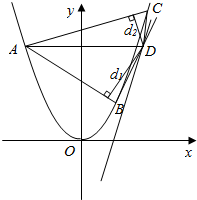
 (理科)如图,A,B,C,D在y=$\frac{1}{4}$x2上,A、D关于抛物线对称轴对称,过点D(x0,y0)作抛物线切线,可证切线斜率为$\frac{1}{2}$x0,BC∥切线,点D到AB,AC距离分别为d1,d2,d1+d2=$\sqrt{2}$|AD|
(理科)如图,A,B,C,D在y=$\frac{1}{4}$x2上,A、D关于抛物线对称轴对称,过点D(x0,y0)作抛物线切线,可证切线斜率为$\frac{1}{2}$x0,BC∥切线,点D到AB,AC距离分别为d1,d2,d1+d2=$\sqrt{2}$|AD|分析 ①利用导数的几何意义即可得出直线BC的斜率,进而可得直线AC、AB的斜率之间的关系,即可判断三角形的形状;
②利用点A的坐标表示弦长|AC|、|AB|,进而利用面积即可得出坐标,及直线方程.
解答 解:①由y=$\frac{1}{4}$x2得,y′=$\frac{1}{2}$x.设D(x0,$\frac{1}{4}$x02),
由导数的几何意义知BC的斜率kBC=$\frac{1}{2}$x0,
由题意知A(-x0,$\frac{1}{4}$x02),设C(x1,$\frac{1}{4}$x12),B(x2,$\frac{1}{4}$x22),
则kBC=$\frac{\frac{1}{4}{(x}_{1}^{2}-{x}_{2}^{2})}{{x}_{1}-{x}_{2}}$=$\frac{1}{4}$(x1+x2)=$\frac{1}{2}$x0,
∴x2=2x0-x1,所以B(2x0-x1,$\frac{1}{4}$(2x0-x1)2),
kAC=$\frac{\frac{1}{4}{(x}_{1}^{2}-{x}_{0}^{2})}{{x}_{1}+{x}_{0}}$=$\frac{1}{4}$(x1-x0),kAB=$\frac{\frac{1}{4}{(x}_{2}^{2}-{x}_{0}^{2})}{{x}_{2}+{x}_{0}}$=$\frac{1}{4}$(x2-x0)=$\frac{1}{4}$(x0-x1),
所以kAC=-kAB,
∴∠DAC=∠DAB,
∴d1=d2,
又由d1+d2=$\sqrt{2}$|AD|得:sin∠DAC=$\frac{\sqrt{2}}{2}$,
∴∠DAC=∠DAB=45°,
故△ABC是直角三角形.
②由①知,不妨设C在AD上方,AB的方程为:y-$\frac{1}{4}$x02=-(x+x0),
由$\left\{\begin{array}{l}y-\frac{1}{4}{x}_{0}^{2}=-(x+{x}_{0})\\{y=\frac{1}{4}x}^{2}\end{array}\right.$得到另一个交点B(x0-4,$\frac{1}{4}$(x0-4)2).
由AC方程为:y-$\frac{1}{4}$x02=x+x0,
由$\left\{\begin{array}{l}y-\frac{1}{4}{x}_{0}^{2}=x+{x}_{0}\\{y=\frac{1}{4}x}^{2}\end{array}\right.$得到另一个交点C(x0+4,$\frac{1}{4}$(x0+4)2).
∴|AB|=$\sqrt{2}$|(x0-4)-(-x0)|=$\sqrt{2}$|2x0-4|,
|AC|=$\sqrt{2}$|(x0+4)-(-x0)|=$\sqrt{2}$|2x0+4|,
∴S△ABC=$\frac{1}{2}$•2|2x0-4||2x0+4|=240,
解得x0=±8,
∴A(8,16)或(-8,16),
若x0=8时,B(4,4),C(12,36),BC:y=4x-12,
若x0=-8时,B(-12,36),C(-4,4),BC:y=-4x-12.
点评 熟练掌握导数的几何意义、直线的斜率与倾斜角的关系、直线与抛物线相交问题、弦长公式即可得出.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | μ=$\frac{k-n}{k-m}$ | B. | μ=$\frac{n-m}{n-k}$ | C. | μ=$\frac{n-m}{k-m}$ | D. | μ=$\frac{k-m}{k-n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com