已知数列
满足
（
为常数），
成等差数列.
（Ⅰ）求p的值及数列的通项公式；
（Ⅱ）设数列
满足
，证明：
.
解：（Ⅰ）由
得
∵成等差数列，
∴
即
得
………………………………………（2分）
依题意知，
当
时，
…
相加得
∴
∴
……………………………………………………………（4分）
又
适合上式， ………………………………………………………（5分）
故
……………………………………………………………………（6分）
（Ⅱ）证明：∵
∴
∵
…………………（8分）
若
则
即当时，有
…………………………………………………（10分）
又因为
………………………………………………………（11分）
故
……………………………………………………………………（12分）
（Ⅱ）法二：要证
只要证
…………………………………………………………（7分）
下面用数学归纳法证明：
①当
时，左边=12，右边=9，不等式成立；
当
时，左边=36，右边=36，不等式成立.…………………………（8分）
②假设当
时，
成立. …………………（9分）
则当
时，左边=4×3k+1=3×4×3k≥3×9k2，
要证3×9k2≥9（k+1）2 ，
只要正3k2≥（k+1）2 ，
即证2k2-2k-1≥0.…………………………………………………………（10分）
而当k
即
且
时，上述不等式成立.………………（11分）
由①②可知，对任意
，所证不等式成立.…
科目：高中数学 来源：2012-2013学年山东临沂高三5月高考模拟理科数学试卷（解析版） 题型：解答题
已知数列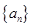
满足
（
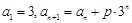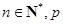为常数），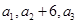
成等差数列.
（Ⅰ）求p的值及数列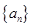的通项公式；
（Ⅱ）设数列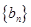
满足
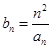，证明：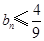
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
满足
（
为常数，
），若
，则
．
满足
（
为常数，
），若
，则
．
满足
（
为常数，
），若
，则
▲ ．