
【题目】解答题
(Ⅰ)已知函数f(x)=|x+1|+|x﹣a|(a>0),若不等式f(x)≥5的解集为{x|x≤﹣2或x≥3},求a的值;
(Ⅱ) 已知实数a,b,c∈R+ , 且a+b+c=m,求证: ![]() +
+ ![]() +
+ ![]() ≥
≥ ![]() .
.
【答案】解:(Ⅰ) 因为a>0,所以 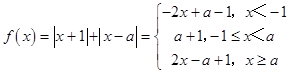 , 又因为不等式f(x)≥5的解集为{x|x≤﹣2或x≥3},就是x=﹣2或x=3时,f(x)=5,解得a=2.(5分)
, 又因为不等式f(x)≥5的解集为{x|x≤﹣2或x≥3},就是x=﹣2或x=3时,f(x)=5,解得a=2.(5分)
(Ⅱ)证明: 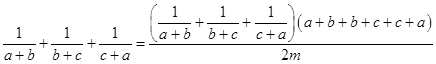
= 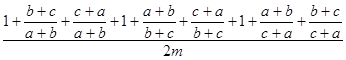
= 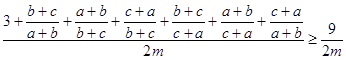
【解析】(Ⅰ)化简函数f(x)=|x+1|+|x﹣a|(a>0)为分段函数,然后通过不等式f(x)≥5的解集为{x|x≤﹣2或x≥3},求a的值;(Ⅱ)利用“1”的代换,利用基本不等式转化证明即可.
【考点精析】解答此题的关键在于理解不等式的证明的相关知识,掌握不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
.
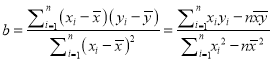 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2) ![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应市政府“绿色出行”的号召,王老师每个工作日上下班由自驾车改为选择乘坐地铁或骑共享单车这两种方式中的一种出行.根据王老师从2017年3月到2017年5月的出行情况统计可知,王老师每次出行乘坐地铁的概率是0.4,骑共享单车的概率是0.6.乘坐地铁单程所需的费用是3元,骑共享单车单程所需的费用是1元.记王老师在一个工作日内上下班所花费的总交通费用为X元,假设王老师上下班选择出行方式是相互独立的.
(I)求X的分布列和数学期望 ![]() ;
;
(II)已知王老师在2017年6月的所有工作日(按22个工作日计)中共花费交通费用110元,请判断王老师6月份的出行规律是否发生明显变化,并依据以下原则说明理由.
原则:设 ![]() 表示王老师某月每个工作日出行的平均费用,若
表示王老师某月每个工作日出行的平均费用,若 ![]() ,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注:
,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋中装有2个白球和n(n≥2,n ![]() N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
(I)用含n的代数式表示1次摸球中奖的概率;
(Ⅱ)若n=3,求3次摸球中恰有1次中奖的概率;
(III)记3次摸球中恰有1次中奖的概率为f(p),当f(p)取得最大值时,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=cos2x的图象向左平移 ![]() 个单位,得到函数y=f(x)cosx的图象,则f(x)的表达式可以是( )
个单位,得到函数y=f(x)cosx的图象,则f(x)的表达式可以是( )
A.f(x)=﹣2sinx
B.f(x)=2sinx
C.f(x)= ![]() sin2x
sin2x
D.f(x)= ![]() (sin2x+cos2x)
(sin2x+cos2x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的最小值为3,且
的最小值为3,且![]() .
.
求函数![]() 的解析式;
的解析式;
(2)若偶函数![]() (其中
(其中![]() ),那么,
),那么, ![]() 在区间
在区间![]() 上是否存在零点?请说明理由.
上是否存在零点?请说明理由.
【答案】(1)![]() (2)存在零点
(2)存在零点
【解析】试题分析:(1)待定系数法,己知函数类型为二次函数,又知f(-1)=f(3),所以对称轴是x=1,且函数最小值f(1)=3,所设函数![]() ,且
,且![]() ,代入f(-1)=11,可解a。
,代入f(-1)=11,可解a。
(2)由题意可得![]() ,代入
,代入![]() ,由
,由![]() 和根的存在性定理,
和根的存在性定理, ![]() 在区间(1,2)上存在零点。
在区间(1,2)上存在零点。
试题解析:(1)因为![]() 是二次函数,且
是二次函数,且![]()
所以二次函数图像的对称轴为![]() .
.
又![]() 的最小值为3,所以可设
的最小值为3,所以可设![]() ,且
,且![]()
由![]() ,得
,得![]()
所以![]()
(2)由(1)可得![]() ,
,
因为![]() ,
,
![]()
所以![]() 在区间(1,2)上存在零点.
在区间(1,2)上存在零点.
【点睛】
(1)对于求己知类型函数的的解析式,常用待定系数法,由于二次函数的表达式形式比较多,有一般式,两点式,顶点式,由本题所给条件知道对称轴与顶点坐标,所以设顶点式。
(2)对于判定函数在否存在零点问题,一般解决此类问题的三步曲是:①先通过观察函数图象再估算出根所在的区间;②根据方程根的存在性定理证明根是存在的;③最后根据函数的性质证明根是唯一的.本题给了区间,可直接用根的存在性定理。
【题型】解答题
【结束】
20
【题目】《中华人民共和国个人所得税》规定,公民月工资、薪金所得不超过3500元的部分不纳税,超过3500元的部分为全月税所得额,此项税款按下表分段累计计算:
全月应纳税所得额 | 税率 |
不超过1500元的部分 |
|
超过1500元至4500元的部分 |
|
超过4500元至9000元的部分 |
|
(1)已知张先生的月工资,薪金所得为10000元,问他当月应缴纳多少个人所得税?
(2)设王先生的月工资,薪金所得为![]() ,当月应缴纳个人所得税为
,当月应缴纳个人所得税为![]() 元,写出
元,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)已知王先生一月份应缴纳个人所得税为303元,那么他当月的工资、薪金所得为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王、小张两位同学玩投掷正四面体(每个面都为等边三角形的正三棱锥)骰子(骰子质地均匀,各面上的点数分别为![]() )游戏,规则:小王现掷一枚骰子,向下的点数记为
)游戏,规则:小王现掷一枚骰子,向下的点数记为![]() ,小张后掷一枚骰子,向下的点数记为
,小张后掷一枚骰子,向下的点数记为![]() ,
,
(1)在直角坐标系![]() 中,以
中,以![]() 为坐标的点共有几个?试求点
为坐标的点共有几个?试求点![]() 落在直线
落在直线![]() 上的概率;
上的概率;
(2)规定:若![]() ,则小王赢,若
,则小王赢,若![]() ,则小张赢,其他情况不分输赢,试问这个游戏公平吗?请说明理由.
,则小张赢,其他情况不分输赢,试问这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com