
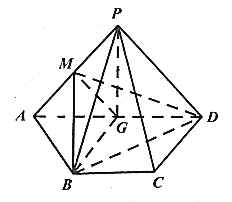
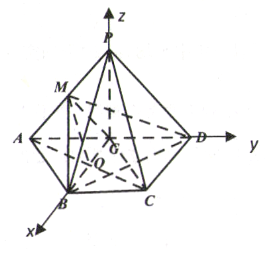
【题目】如图,已知四边形![]() 的直角梯形,
的直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点(
上一点(![]() 不与端点重合).
不与端点重合).
(Ⅰ)若![]() ,
,
(i)求证:![]() 平面
平面![]() ;
;
(ii)求直线![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(Ⅱ)否存在实数![]() 满足
满足![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐角为
所成的锐角为![]() ,若存在,确定
,若存在,确定![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(Ⅰ)(i)见解析(ii)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)(i)先根据平行四边形性质得![]() ,再根据线面平行判定定理得结果,(ii)先根据条件建立空间直角坐标系,设立各点坐标,列方程组解得平面
,再根据线面平行判定定理得结果,(ii)先根据条件建立空间直角坐标系,设立各点坐标,列方程组解得平面![]() 的法向量,根据向量数量积得向量夹角,最后根据线面角与向量夹角关系得结果.(Ⅱ)先根据条件建立空间直角坐标系,设立各点坐标,列方程组解得两平面法向量,根据向量数量积得向量夹角,最后根据二面角与向量夹角关系得结果.
的法向量,根据向量数量积得向量夹角,最后根据线面角与向量夹角关系得结果.(Ⅱ)先根据条件建立空间直角坐标系,设立各点坐标,列方程组解得两平面法向量,根据向量数量积得向量夹角,最后根据二面角与向量夹角关系得结果.
(Ⅰ)(i)证明:连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,依题意易证四边形
,依题意易证四边形![]() 为平行四边形.
为平行四边形.
∴![]() 又∵
又∵![]() ,
,
∴![]() 又∵
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
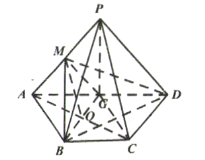
(ii)解:如图,在平行四边形![]() 中∵
中∵![]() ,
,![]() ,∴
,∴![]()
以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]()
则![]() ,
,
![]()
∴![]()
设![]() 为平面
为平面![]() 的法向量
的法向量
则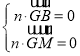 ,得
,得![]() ,不妨设
,不妨设![]()
∴![]()
又![]() ,∴
,∴![]()
即直线![]() 与平面
与平面![]() 所成的角的大小为
所成的角的大小为![]() .
.
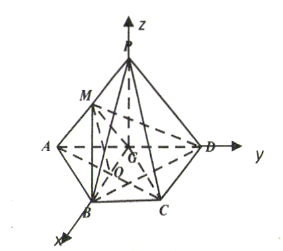
(Ⅱ)设![]()
∴![]()
∴![]()
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则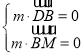 得,
得,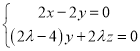 ,不妨设
,不妨设![]() ,
,
又平面![]() 的法向量为
的法向量为![]() ,
,
∴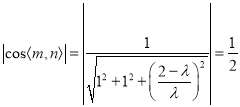 .
.
∴![]() ∴
∴![]() ,
,![]() ,∴
,∴![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
【题目】江夏一中将要举行校园歌手大赛,现有3男3女参加,需要安排他们的出场顺序.(结果用数字作答)
(1)如果3个女生都不相邻,那么有多少种不同的出场顺序?
(2)如果女生甲在女生乙的前面(可以不相邻),那么有多少种不同的出场顺序?
(3)如果3位男生都相邻,且女生甲不在第一个出场,那么有多少种不同的出场顺序?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
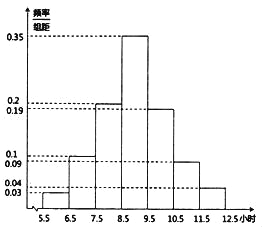
(1)求这200名学生每周阅读时间的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);
(2)由直方图可以认为,目前该校学生每周的阅读时间![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若![]() ,令
,令![]() ,则
,则![]() ,且
,且![]() .利用直方图得到的正态分布,求
.利用直方图得到的正态分布,求![]() .
.
(ii)从该高校的学生中随机抽取20名,记![]() 表示这20名学生中每周阅读时间超过10小时的人数,求
表示这20名学生中每周阅读时间超过10小时的人数,求![]() (结果精确到0.0001)以及
(结果精确到0.0001)以及![]() 的数学期望.
的数学期望.
参考数据:![]() ,
,![]() .若
.若![]() ,则
,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com