
【题目】设函数f(x)=lnx+ ![]() ,m∈R,若对任意b>a>0,
,m∈R,若对任意b>a>0, ![]() <1恒成立,则m的取值范围为 .
<1恒成立,则m的取值范围为 .
【答案】[ ![]() ,+∞)
,+∞)
【解析】(Ⅲ)对任意b>a>0, ![]() <1恒成立,
<1恒成立,
等价于f(b)﹣b<f(a)﹣a恒成立;
设h(x)=f(x)﹣x=lnx+ ![]() ﹣x(x>0),
﹣x(x>0),
则h(b)<h(a).
∴h(x)在(0,+∞)上单调递减;
∵h′(x)= ![]() ﹣
﹣ ![]() ﹣1≤0在(0,+∞)上恒成立,
﹣1≤0在(0,+∞)上恒成立,
∴m≥﹣x2+x=﹣(x﹣ ![]() )2+
)2+ ![]() (x>0),
(x>0),
∴m≥ ![]() ;
;
对于m= ![]() ,h′(x)=0仅在x=
,h′(x)=0仅在x= ![]() 时成立;
时成立;
∴m的取值范围是[ ![]() ,+∞).
,+∞).
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为[﹣1,5],部分对应值如表,
x | ﹣1 | 0 | 4 |
f(x) | 1 | 2 | 2 |
f(x)的导函数y=f′(x)的图象(该图象关于(2,0)中心对称) 如图所示.
下列关于f(x)的命题:
①函数f(x)的极大值点为 0与4;
②函数f(x)在[0,2]上是减函数;
③函数y=f(x)﹣a零点的个数可能为0、1、2、3、4个;
④如果当时x∈[﹣1,t],f(x)的最大值是2,那么t的最大值为5;.
⑤函数f(x)的图象在a=1是上凸的
其中一定正确命题的序号是 . 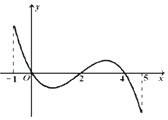
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|x﹣3|+|x﹣4|. (Ⅰ)解不等式f(x)≤2;
(Ⅱ)若对任意实数x∈[5,9],f(x)≤ax﹣1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A= ![]() ,B={y|y=log2x,4<x<16},
,B={y|y=log2x,4<x<16}, 
(1)求图中阴影部分表示的集合C;
(2)若非空集合D={x|4﹣a<x<a},且D(A∪B),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[ ![]() ]表示不超过
]表示不超过 ![]() 的最大整数.若 S1=[
的最大整数.若 S1=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=3,
]=3,
S2=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=10,
]=10,
S3=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=21,
]=21,
…,
则Sn=( )
A.n(n+2)
B.n(n+3)
C.(n+1)2﹣1
D.n(2n+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3sin(ωx+) ![]() 的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )
的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( ) 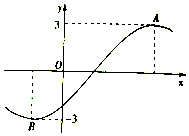
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+3在(﹣∞,1]上是减函数,当x∈[a+1,1]时,f(x)的最大值与最小值之差为g(a),则g(a)的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com