
分析 先明白题目所给解答的方法,然后依照所给定义解答题目即可.
解答 解:$\frac{k}{x+a}+\frac{x+b}{x+c}$<0解集为(-3,-2)∪(1,2),
用-$\frac{1}{x}$替换x,不等式可以化为:$\frac{kx}{ax-1}$+$\frac{bx-1}{cx-1}$<0
可得-$\frac{1}{x}$∈(-3,-2)∪(1,2),
可得$\frac{1}{2}$<x<1或-$\frac{1}{2}$<x<-$\frac{1}{3}$.
故答案为:($\frac{1}{2}$,1)∪(-$\frac{1}{2}$,-$\frac{1}{3}$)
点评 本题是创新题目,考查理解能力,读懂题意是解答本题关键,将方程问题和不等式问题进行转化是解答本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
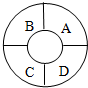 有4种不同的备选颜色给如图示的A、B、C、D四块涂色,要求每块涂同一种颜色,且相邻两块涂不同的颜色,则不同的涂色方法有( )种.
有4种不同的备选颜色给如图示的A、B、C、D四块涂色,要求每块涂同一种颜色,且相邻两块涂不同的颜色,则不同的涂色方法有( )种.| A. | 48 | B. | 60 | C. | 84 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com