
【题目】已知平面向量![]() ,满足
,满足![]() 且
且![]() ,若对每一个确定的向量
,若对每一个确定的向量![]() ,记
,记![]() 的最小值为
的最小值为![]() ,则当
,则当![]() 变化时,
变化时,![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
【答案】B
【解析】
根据题意,建立平面直角坐标系.令![]()
![]() .
.![]() 为
为![]() 中点.由
中点.由![]() 即可求得
即可求得![]() 点的轨迹方程.将
点的轨迹方程.将![]() 变形,结合
变形,结合![]() 及平面向量基本定理可知
及平面向量基本定理可知![]() 三点共线.由圆切线的性质可知
三点共线.由圆切线的性质可知![]() 的最小值
的最小值![]() 即为
即为![]() 到直线
到直线![]() 的距离最小值,且当
的距离最小值,且当![]() 与圆
与圆![]() 相切时,
相切时,![]() 有最大值.利用圆的切线性质及点到直线距离公式即可求得直线方程,进而求得原点到直线的距离,即为
有最大值.利用圆的切线性质及点到直线距离公式即可求得直线方程,进而求得原点到直线的距离,即为![]() 的最大值.
的最大值.
根据题意,![]() 设
设![]() ,
,![]()
则![]()
由![]() 代入可得
代入可得![]()
即![]() 点的轨迹方程为
点的轨迹方程为![]()
又因为![]() ,变形可得
,变形可得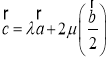 ,即
,即![]() ,且
,且![]()
所以由平面向量基本定理可知![]() 三点共线,如下图所示:
三点共线,如下图所示:
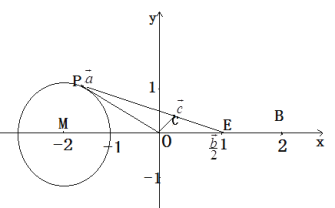
所以![]() 的最小值
的最小值![]() 即为
即为![]() 到直线
到直线![]() 的距离最小值
的距离最小值
根据圆的切线性质可知,当![]() 与圆
与圆![]() 相切时,
相切时,![]() 有最大值
有最大值
设切线![]() 的方程为
的方程为![]() ,化简可得
,化简可得![]()
由切线性质及点![]() 到直线距离公式可得
到直线距离公式可得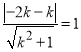 ,化简可得
,化简可得![]()
即![]()
所以切线方程为![]() 或
或![]()
所以当![]() 变化时,
变化时, ![]() 到直线
到直线![]() 的最大值为
的最大值为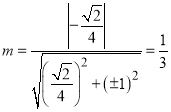
即![]() 的最大值为
的最大值为![]()
故选:B


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是一个菱形,三角形PAD是一个等腰三角形,∠BAD=∠PAD=![]() ,点E在线段PC上,且PE=3EC.
,点E在线段PC上,且PE=3EC.
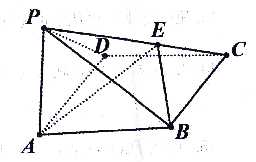
(1)求证:AD⊥PB;
(2)若平面PAD⊥平面ABCD,求二面角E﹣AB﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且a+b+c=8.
(1)若a=2,b=![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2![]() +sinB·cos2
+sinB·cos2![]() =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S=![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的长为2,宽为1,
的长为2,宽为1, ![]() ,
, ![]() 边分别在
边分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上, ![]() 点与坐标原点重合,将矩形折叠,使
点与坐标原点重合,将矩形折叠,使![]() 点落在线段
点落在线段![]() 上,设此点为
上,设此点为![]() .
.
(1)若折痕的斜率为-1,求折痕所在的直线的方程;
(2)若折痕所在直线的斜率为![]() ,(
,( ![]() 为常数),试用
为常数),试用![]() 表示点
表示点![]() 的坐标,并求折痕所在的直线的方程;
的坐标,并求折痕所在的直线的方程;
(3)当![]() 时,求折痕长的最大值.
时,求折痕长的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《数书九章》是中国南宋时期杰出数学家秦九韶的著作,其中在卷五“三斜求积”中提出了已知三角形三边![]() 、
、![]() 、
、![]() ,求面积的公式,这与古希腊的海伦公式完全等价,其求法是“以小斜冥并大斜冥减中斜冥,余半之,自乘于上,以小斜冥乘大斜冥减上,余四约之,为实.一为从隅,开平方得积”若把以上这段文字写出公式,即若
,求面积的公式,这与古希腊的海伦公式完全等价,其求法是“以小斜冥并大斜冥减中斜冥,余半之,自乘于上,以小斜冥乘大斜冥减上,余四约之,为实.一为从隅,开平方得积”若把以上这段文字写出公式,即若![]() ,则
,则![]() .
.
(1)已知![]() 的三边
的三边![]() ,
,![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() 的面积
的面积![]() .
.
(2)若![]() ,
,![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,方程![]() (为
(为![]() ,
,![]() 为不相等的两个正数)所代表的曲线是( )
为不相等的两个正数)所代表的曲线是( )
A. 三角形 B. 正方形 C. 非正方形的长方形 D. 非正方形的菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com