
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 4 |
| 9 |
| 1 |
| 4 |
| 4 |
| 9 |
| 1 |
| 2 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 5 |
| 9 |
| 125 |
| 729 |
| 4 |
| 9 |
| 5 |
| 9 |
| 100 |
| 243 |
| 4 |
| 9 |
| 5 |
| 9 |
| 80 |
| 243 |
| 4 |
| 9 |
| 64 |
| 729 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求一个试验组为甲类组的概率;
(2)观察3个试验组,用ξ表示这3个试验组中甲类组的个数,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为![]() ,服用B有效的概率为
,服用B有效的概率为![]() 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用![]() 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海交大附中高三数学理总复习二概率等练习卷(解析版) 题型:解答题
设A,B是治疗同一种疾病的两种药,用若干试验组进行对比试验.每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效.若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的只数多,就称该试验组为甲类组.设每只小白鼠服用A有效的概率为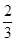 ,服用B有效的概率为
,服用B有效的概率为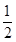 .
.
(1)求一个试验组为甲类组的概率;
(2)观察三个试验组,用X表示这三个试验组中甲类组的个数,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com