
| |||||||||||
(1) |
解:由已知得F1(-1,0)…………1分 ∵ ∴MP为线段NF2的垂直平分线……2分 ∴│MN│=│MF2│…………3分 由椭圆的定义知:│MF1│+│MF2│=2 ∴│NF1│=│MN│+│MF1│=│MF2│+│MF1│=2 设N(x,y),则(x+1)2+y2=8…………6分 显然M为椭圆左、右端点时不满足 ∴曲线E的方程为(x+1)2+y2=8(y≠0)…………7分 |
(2) |
解:由⑴知│F1H│=2 ∵ ∴│F1G│= ∴G点的轨迹是以F1(-1,0)为圆心, ∴G点轨迹方程是(x+1)2+y2=2(y>0)…………11分 又∵G在椭圆上: 由 ∴G(0,1)…………13分 ∴所求的直线方程为:y=x+1…………14分 |


科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知f1(x)=Asin(ωx+![]() )(A>0,ω>0,|
)(A>0,ω>0,|![]() |<
|<![]() )的部分图象如下图所示:
)的部分图象如下图所示:
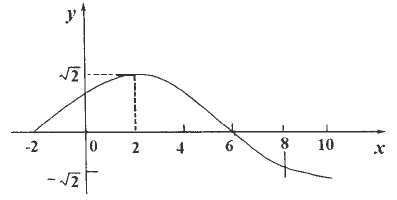
(1)求此函数的解析式f1(x);
(2)与f1(x)的图象关于x=8对称的函数解析式f2(x);求f1(x)+f2(x)单增区间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com