
°æƒø°ø£®±æ–°Ã‚¬˙∑÷13∑÷£©»ÁÕºÀ˘ 浃敓∂Õºº«¬º¡Àº◊°¢““¡Ω◊È∏˜Àƒ√˚Õ¨—ßµƒÕ∂¿∫√¸÷–¥Œ ˝, ““◊Ⱥ«¬º÷–”–“ª∏ˆ ˝æðƒ£∫˝£¨ŒÞ∑®»∑»œ, ‘⁄Õº÷–“‘![]() ±Ì æ.
±Ì æ.

£®¢Ò£©»Áπ˚““◊ÈÕ¨—ßÕ∂¿∫√¸÷–¥Œ ˝µƒ∆Ωæ˘ ˝Œ™![]() , «Û
, «Û![]() º∞““◊ÈÕ¨—ßÕ∂¿∫√¸÷–¥Œ ˝µƒ∑Ω≤Ó;
º∞““◊ÈÕ¨—ßÕ∂¿∫√¸÷–¥Œ ˝µƒ∑Ω≤Ó;
£®¢Ú£©‘⁄£®¢Ò£©µƒÃıº˛œ¬, ∑÷±¥”º◊°¢““¡Ω◊ÈÕ∂¿∫√¸÷–¥Œ ˝µÕ”⁄10¥ŒµƒÕ¨—ß÷–,∏˜Àʪ˙—°»°“ª√˚, º« ¬º˛A£∫°∞¡Ω√˚Õ¨—ßµƒÕ∂¿∫√¸÷–¥Œ ˝÷Æ∫ÕŒ™17°±, «Û ¬º˛A∑¢…˙µƒ∏≈¬ .
°æ¥∞∏°ø£®¢Ò£©![]() £¨
£¨![]() £ª£®¢Ú£©
£ª£®¢Ú£©![]() .
.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®¢Ò£©¿˚”√∆Ωæ˘ ˝π´ Ωº¥ø…«Ûµ√x,¿˚”√∑Ω≤Óµƒº∆À„π´ Ωº¥ø…«Ûµ√∑Ω≤Ó
£®¢Ú£©¡–≥ˆ’‚¡Ω√˚Õ¨—ßµƒÕ∂¿∫√¸÷–¥Œ ˝÷Æ∫ÕŒ™17µƒÀ˘“‘ ±º‰¿˚”√π≈µ‰∏≈–Õº¥ø…«Û≥ˆ∏≈¬
‘Ã‚Ω‚Œˆ£∫£®¢Ò£©”…Âø…µ√![]() £¨
£¨
∑Ω≤Ó![]()
£®¢Ú£©º«º◊◊ÈÕ∂¿∫√¸÷–¥Œ ˝µÕ”⁄10¥ŒµƒÕ¨—ߌ™![]() £¨À˚√«µƒÕ∂¿∫√¸÷–¥Œ ˝∑÷±Œ™9,7
£¨À˚√«µƒÕ∂¿∫√¸÷–¥Œ ˝∑÷±Œ™9,7
º«““◊ÈÕ∂¿∫√¸÷–¥Œ ˝µÕ”⁄10¥ŒµƒÕ¨—ß![]() £¨À˚√«µƒÕ∂¿∫√¸÷–¥Œ ˝∑÷±Œ™8£¨8,9£¨”…“‚
£¨À˚√«µƒÕ∂¿∫√¸÷–¥Œ ˝∑÷±Œ™8£¨8,9£¨”…“‚
≤ªÕ¨µƒ—°»°∑Ω∑®”–![]() π≤6÷÷£¨
π≤6÷÷£¨
…Ë°∞’‚¡Ω√˚Õ¨—ßµƒÕ∂¿∫√¸÷–¥Œ ˝÷Æ∫ÕŒ™17°±Œ™ ¬º˛![]() £¨‘Ú
£¨‘Ú![]() ÷–∫¨”–
÷–∫¨”–![]() π≤2÷÷ª˘±æ ¬º˛
π≤2÷÷ª˘±æ ¬º˛
π ![]()


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº◊≤Œº”A £¨ B £¨ C»˝∏ˆø∆ƒøµƒ—ß“µÀÆ∆Ωøº ‘£¨∆‰øº ‘≥…º®∫œ∏Òµƒ∏≈¬ »Áœ¬±Ì£¨ºŸ…Ë»˝∏ˆø∆ƒøµƒøº ‘º◊ «∑Ò≥…º®∫œ∏Òœýª•∂¿¡¢£Æ
ø∆ƒøA | ø∆ƒøB | ø∆ƒøC | |
º◊ |
|
|
|
£®I£©«Ûº◊÷¡…Ÿ”–“ª∏ˆø∆ƒøøº ‘≥…º®∫œ∏Òµƒ∏≈¬ £ª
£®¢Ú£©…˺◊≤Œº”øº ‘≥…º®∫œ∏Òµƒø∆ƒø ˝¡øŒ™X £¨ «ÛXµƒ∑÷≤º¡–∫Õ ˝—ß∆⁄Õ˚£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() µƒÕºœÒ «”…∫Ø ˝
µƒÕºœÒ «”…∫Ø ˝![]() µƒÕºœÒæ≠»Áœ¬±‰ªªµ√µΩ£∫œ»Ω´
µƒÕºœÒæ≠»Áœ¬±‰ªªµ√µΩ£∫œ»Ω´![]() ÕºœÒ…œÀ˘”–µ„µƒ◊ð◊¯±Í…Ï≥§µΩ‘≠¿¥µƒ2±∂£®∫·◊¯±Í≤ª±‰£©£¨‘ŸΩ´À˘µ√µΩµƒÕºœÒœÚ”“∆Ω“∆
ÕºœÒ…œÀ˘”–µ„µƒ◊ð◊¯±Í…Ï≥§µΩ‘≠¿¥µƒ2±∂£®∫·◊¯±Í≤ª±‰£©£¨‘ŸΩ´À˘µ√µΩµƒÕºœÒœÚ”“∆Ω“∆![]() ∏ˆµ•Œª≥§∂».
∏ˆµ•Œª≥§∂».
£®¢Ò£©«Û∫Ø ˝![]() µƒΩ‚Œˆ Ω£¨≤¢«Û∆‰ÕºœÒµƒ∂‘≥∆÷·∑Ω≥ãª
µƒΩ‚Œˆ Ω£¨≤¢«Û∆‰ÕºœÒµƒ∂‘≥∆÷·∑Ω≥ãª
£®¢Ú£©“—÷™πÿ”⁄![]() µƒ∑Ω≥Ã
µƒ∑Ω≥Ã![]() ‘⁄
‘⁄![]() ƒ⁄”–¡Ω∏ˆ≤ªÕ¨µƒΩ‚
ƒ⁄”–¡Ω∏ˆ≤ªÕ¨µƒΩ‚![]() £Æ
£Æ
£®1£©«Û µ ˝mµƒ»°÷µ∑∂Œß£ª
£®2£©÷§√˜£∫![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄»˝¿‚◊∂PABC÷–£¨D£¨E£¨F∑÷±Œ™¿‚PC£¨AC£¨ABµƒ÷–µ„£¨“—÷™PA°ÕAC£¨PA=6£¨BC=8£¨DF=5£Æ«Û÷§£∫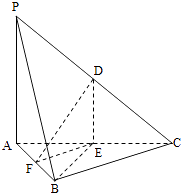
£®1£©÷±œþPA°Œ∆Ω√ÊDEF£ª
£®2£©∆Ω√ÊBDE°Õ∆Ω√ÊABC£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“ª∏ˆ»ð¡øŒ™Mµƒ—˘±æ ˝æð£¨∆‰∆µ¬ ∑÷≤º±Ì»Áœ¬£Æ
£®1£©º∆À„a,bµƒ÷µ;
£®2£©ª≠≥ˆ∆µ¬ ∑÷≤º÷±∑ΩÕº£ª
£®3£©”√∆µ¬ ∑÷≤º÷±∑ΩÕº£¨«Û≥ˆ◊Ðõƒ÷⁄ ˝º∞∆Ωæ˘ ˝µƒπ¿º∆÷µ£Æ
∆µ¬ ∑÷≤º±Ì
∑÷◊È | ∆µ ˝ | ∆µ¬ | ∆µ¬ /◊Èæý |
(10,20] | 2 | 0.10 | 0.010 |
(20,30] | 3 | 0.15 | 0.015 |
(30,40] | 4 | 0.20 | 0.020 |
(40,50] | a | b | 0.025 |
(50,60] | 4 | 0.20 | 0.020 |
(60, 70] | 2 | 0.10 | 0.010 |

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=Asin£®¶ÿx+¶’£© £®A£æ0£¨¶ÿ£æ0£¨0£º¶’£º¶–£©£¨∆‰µº∫Ø ˝f°‰£®x£©µƒ≤ø∑÷ÕºœÛ»ÁÕºÀ˘ 棨‘Ú∫Ø ˝f£®x£©µƒΩ‚Œˆ ΩŒ™£® £© 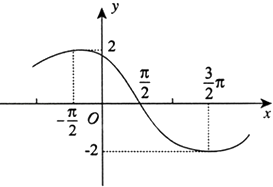
A.f£®x£©=4sin£® ![]() x+
x+ ![]() ¶–£©
¶–£©
B.f£®x£©=4sin£® ![]() x+
x+ ![]() £©
£©
C.f£®x£©=4sin£® ![]() x+
x+ ![]() £©
£©
D.f£®x£©=4sin£® ![]() x+
x+ ![]() £©
£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∫Ø ˝![]() µƒ“ª∂ŒÕºœÛ»ÁÕºÀ˘ æ£∫Ω´
µƒ“ª∂ŒÕºœÛ»ÁÕºÀ˘ æ£∫Ω´![]() µƒÕºœÛœÚ”“∆Ω“∆
µƒÕºœÛœÚ”“∆Ω“∆![]() £®
£®![]() £©∏ˆµ•Œª£¨ø…µ√µΩ∫Ø ˝
£©∏ˆµ•Œª£¨ø…µ√µΩ∫Ø ˝![]() µƒÕºœÛ£¨«“ÕºœÛπÿ”⁄‘≠µ„∂‘≥∆.£®1£©«Û
µƒÕºœÛ£¨«“ÕºœÛπÿ”⁄‘≠µ„∂‘≥∆.£®1£©«Û![]() µƒ÷µ.
µƒ÷µ.
£®2£©«Û![]() µƒ◊Ó–°÷µ£¨≤¢–¥≥ˆ
µƒ◊Ó–°÷µ£¨≤¢–¥≥ˆ![]() µƒ±Ì¥Ô Ω.
µƒ±Ì¥Ô Ω.
(3)…Ët>0,πÿ”⁄xµƒ∫Ø ˝![]() ‘⁄«¯º‰
‘⁄«¯º‰![]() …œ◊Ó–°÷µŒ™-2£¨«Ûtµƒ∑∂Œß.
…œ◊Ó–°÷µŒ™-2£¨«Ûtµƒ∑∂Œß.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë ˝¡–{an}µƒ«∞nœÓ∫ÕŒ™Sn £Æ »ÙSn=2an©Ån£¨‘Ú ![]() +
+ ![]() +
+ ![]() +
+ ![]() = £Æ
= £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®±æ–°Ã‚¬˙∑÷12∑÷£©Œ“√«∞—“ªœµ¡–œÚ¡ø![]() ∞¥¥Œ–Ú≈≈≥…“ª¡–£¨≥∆÷ÆŒ™œÚ¡ø¡–£¨º«◊˜
∞¥¥Œ–Ú≈≈≥…“ª¡–£¨≥∆÷ÆŒ™œÚ¡ø¡–£¨º«◊˜![]() £¨“—÷™œÚ¡ø¡–
£¨“—÷™œÚ¡ø¡–![]() ¬˙◊„£∫
¬˙◊„£∫![]() £¨
£¨![]()
![]() £Æ
£Æ
£®1£©÷§√˜£∫ ˝¡–![]() «µ»±» ˝¡–£ª
«µ»±» ˝¡–£ª
£®2£©…Ë![]() ±Ì æœÚ¡ø
±Ì æœÚ¡ø![]() ”Î
”Î![]() º‰µƒº–Ω«£¨»Ù
º‰µƒº–Ω«£¨»Ù![]() £¨∂‘”⁄»Œ“‚’˝’˚ ˝
£¨∂‘”⁄»Œ“‚’˝’˚ ˝![]() £¨≤ªµ» Ω
£¨≤ªµ» Ω ∫„≥…¡¢£¨«Û µ ˝
∫„≥…¡¢£¨«Û µ ˝![]() µƒ∑∂Œß
µƒ∑∂Œß
£®3£©…Ë![]() £¨Œ ˝¡–
£¨Œ ˝¡–![]() ÷– «∑ҥʑ⁄◊Ó–°œÓ£ø»Ù¥Ê‘⁄£¨«Û≥ˆ◊Ó–°œÓ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…
÷– «∑ҥʑ⁄◊Ó–°œÓ£ø»Ù¥Ê‘⁄£¨«Û≥ˆ◊Ó–°œÓ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com