
【题目】设函数f(x)的定义域是(0,+∞),对于任意正实数m,n恒有f(mn)=f(m)+f(n),且当x>1时,f(x)>0,f(2)=1.
(1)求 ![]() 的值;
的值;
(2)求证:f(x)在(0,+∞)上是增函数;
(3)求方程4sinx=f(x)的根的个数.
【答案】
(1)解:令m=n=1,则f(1)=f(1)+f(1),
∴f(1)=0
令 ![]() ,则
,则 ![]() ,
,
∴ ![]()
(2)解:设0<x1<x2,则 ![]()
∵当x>1时,f(x)>0
∴ ![]()
![]()
所以f(x)在(0,+∞)上是增函数
(3)解:∵y=4sinx的图象如右图所示
又f(4)=f(2×2)=2,f(16)=f(4×4)=4
由y=f(x)在(0,+∞)上单调递增,
且f(1)=0,f(16)=4可得y=f(x)的图象大致形状如右图所示,
由图象在[0,2π]内有1个交点,
在(2π,4π]内有2个交点,
在(4π,5π]内有2个交点,又5π<16<6π,
后面y=f(x)的图象均在y=4sinx图象的上方.
故方程4sinx=f(x)的根的个数为5个

【解析】(1)利用赋值法,对于任意正实数m,n恒有f(mn)=f(m)+f(n),可令m=n=1,先求出f(1),然后令 ![]() ,即可求出
,即可求出 ![]() 的值;(2)先在定义域内任取两个值x1 , x2 , 并规定大小,然后判定出f(x1),与f(x2)的大小关系,根据单调增函数的定义可知结论;(3)分别画出y=4sinx的图象与y=f(x)的图象,结合图象以及函数的单调性判定出交点的个数即可.
的值;(2)先在定义域内任取两个值x1 , x2 , 并规定大小,然后判定出f(x1),与f(x2)的大小关系,根据单调增函数的定义可知结论;(3)分别画出y=4sinx的图象与y=f(x)的图象,结合图象以及函数的单调性判定出交点的个数即可.
【考点精析】关于本题考查的函数单调性的判断方法,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】下列命题:
①命题“x∈R,x2+x+1=0”的否定是“x∈R,x2+x+1≠0”;
②若A={x|x>0},B={x|x≤﹣1},则A∩(RB)=A;
③函数f(x)=sin(ωx+φ)(ω>0)是偶函数的充要条件是φ=kπ+ ![]() (k∈Z);
(k∈Z);
④若非零向量 ![]() ,
, ![]() 满足
满足 ![]() =λ
=λ ![]() ,
, ![]() =λ
=λ ![]() (λ∈R),则λ=1.
(λ∈R),则λ=1.
其中正确命题的序号有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l与圆C:x2+y2+2x﹣4y+a=0相交于A,B两点,弦AB的中点为M(0,1).
(1)求实数a的取值范围以及直线l的方程;
(2)若圆C上存在动点N使CN=2MN成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,设动点M(2,t)(t>0).
(1)若过点P(0,4 ![]() )的直线l与圆C:x2+y2﹣8x=0相切,求直线l的方程;
)的直线l与圆C:x2+y2﹣8x=0相切,求直线l的方程;
(2)求以OM为直径且被直线3x﹣4y﹣5=0截得的弦长为2的圆的方程;
(3)设A(1,0),过点A作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上) 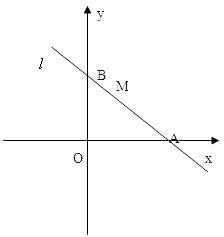
(1)若三角形AOB的面积是4,求直线l的方程.
(2)求过点N(0,1)且与直线l垂直的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
附:

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a≠0,集合A={x|x2﹣x﹣6<0},B={x|x2+2x﹣8≥0},C={x|x2﹣4ax+3a2<0},且C(A∩RB).求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,△ABC是等边三角形,D是AC的中点,PA=PC,二面角P﹣AC﹣B的大小为60°; 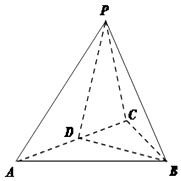
(1)求证:平面PBD⊥平面PAC;
(2)求AB与平面PAC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com