【题目】已知正方形
的中心为点
, 
边所在的直线方程为
.
（1）求
边所在的直线方程和正方形
外接圆的方程；
（2）若动圆
过点
,且与正方形
外接圆外切,求动圆圆心
的轨迹方程.
科目：高中数学 来源： 题型：
【题目】某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．
整理评分数据，将分数以
为组距分成
组： 
， 
， 
， 
， 
， 
，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：
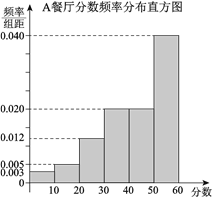
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
定义学生对餐厅评价的“满意度指数”如下：
分数 |
|
|
|
满意度指数 |
|
|
|
（Ⅰ）在抽样的100人中，求对A餐厅评价“满意度指数”为
的人数；
（Ⅱ）从该校在A，B两家餐厅都用过餐的学生中随机抽取1人进行调查，试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率；
（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知cos(75°＋α)＝
，α是第三象限角，
(1)求sin(75°＋α) 的值．
(2）求cos(α－15°) 的值．
(3)求sin(195°－α)+cos(105o－α)的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)是定义在R上的奇函数，当x≥0时，f(x)＝x2－2x.
(1)求f(x)的解析式，并画出f(x)的图象；
(2)设g(x)＝f(x)－k，利用图象讨论：当实数k为何值时，函数g(x)有一个零点？二个零点？三个零点？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，若在定义域内存在
，使得
成立，则称为函数
的局部对称点．
（1）若
，证明：函数
必有局部对称点；
（2）若函数
在区间
内有局部对称点，求实数
的取值范围；
（3）若函数
在
上有局部对称点，求实数
的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
