
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).在以坐标原点为极点
).在以坐标原点为极点![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]()
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)直线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() 满足
满足![]() ,若曲线
,若曲线![]() 与
与![]() 的公共点都在
的公共点都在![]() 上,求
上,求![]() .
.
【答案】(1)圆; ρ2-2ρsin θ+1-a2=0.(2) a=1.
【解析】
(1)根据三角函数平方关系消参数得C1的普通方程,再根据x=ρcos θ,y=ρsin θ化为极坐标方程,(2)联立极坐标方程解得16cos2θ-8sin θcos θ+1-a2=0,再根据tan θ=2化简得1-a2=0,解得a=1.
(1)消去参数t得到C1的普通方程为x2+(y-1)2=a2,则C1是以(0,1)为圆心,a为半径的圆.
将x=ρcos θ,y=ρsin θ代入C1的普通方程中,得到C1的极坐标方程为ρ2-2ρsin θ+1-a2=0.
(2)曲线C1,C2的公共点的极坐标满足方程组![]() ,若ρ≠0,由方程组得16cos2θ-8sin θcos θ+1-a2=0,由已知tan θ=2,得16cos2θ-8sin θcos θ=0,从而1-a2=0,解得a=-1(舍去)或a=1.当a=1时,极点也为C1,C2的公共点,且在C3上.所以a=1.
,若ρ≠0,由方程组得16cos2θ-8sin θcos θ+1-a2=0,由已知tan θ=2,得16cos2θ-8sin θcos θ=0,从而1-a2=0,解得a=-1(舍去)或a=1.当a=1时,极点也为C1,C2的公共点,且在C3上.所以a=1.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C的对边,若△ABC的周长为2(![]() +1),且sin B+sin C=
+1),且sin B+sin C=![]() sin A,则a= ( )
sin A,则a= ( )
A. ![]() B. 2 C. 4 D.
B. 2 C. 4 D. ![]()
【答案】B
【解析】
根据正弦定理把![]() 转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
根据正弦定理,![]() 可化为
可化为![]()
∵△ABC的周长为![]() ,
,
∴联立方程组![]() ,
,
解得a=2.
故选:B
【点睛】
(1)在三角形中根据已知条件求未知的边或角时,要灵活选择正弦、余弦定理进行边角之间的转化,以达到求解的目的.
(2)求角的大小时,在得到角的某一个三角函数值后,还要根据角的范围才能确定角的大小,这点容易被忽视,解题时要注意.
【题型】单选题
【结束】
7
【题目】已知数列{an}中,an=n2-kn(n∈N*),且{an}单调递增,则k的取值范围是( )
A. (-∞,2] B. (-∞,2) C. (-∞,3] D. (-∞,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=![]() AD=1.问:在棱PD上是否存在一点E,使得CE∥平面PAB?若存在,求出E点的位置;若不存在,请说明理由.
AD=1.问:在棱PD上是否存在一点E,使得CE∥平面PAB?若存在,求出E点的位置;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京101中学校园内有一个“少年湖”,湖的两侧有一个音乐教室和一个图书馆,如图,若设音乐教室在A处,图书馆在B处,为测量A,B两地之间的距离,某同学选定了与A,B不共线的C处,构成△ABC,以下是测量的数据的不同方案:①测量∠A,AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B. 其中一定能唯一确定A,B两地之间的距离的所有方案的序号是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A﹣BCD中,侧棱AB、AC、AD两两垂直,△ABC,△ACD,△ADB的面积分别为![]() ,
, ![]() ,
, ![]() , 则三棱锥A﹣BCD的外接球的体积为
, 则三棱锥A﹣BCD的外接球的体积为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.
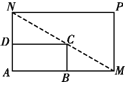
(1)要使矩形AMPN的面积大于9平方米,则DN的长应在什么范围内?
(2)当DN的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x-1)2+(y-2)2=2,过点P(2,-1)作圆C的切线,切点为A,B.
(1)求直线PA,PB的方程;
(2)求过P点的圆C的切线长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com