
【题目】(文科)设函数f(x)=x2﹣2ax﹣8a2(a>0),记不等式f(x)≤0的解集为A.
(1)当a=1时,求集合A;
(2)若(﹣1,1)A,求实数a的取值范围.
【答案】
(1)解:当a=1时,f(x)=x2﹣2x﹣8,
由不等式x2﹣2x﹣8≤0,化为(x﹣4)(x+2)≤0,
解得﹣2≤x≤4,
∴集合A={x|﹣2≤x≤4}
(2)解:∵x2﹣2ax﹣8a2≤0,
∴(x﹣4a)(x+2a)≤0,
又∵a>0,∴﹣2a≤x≤4a,∴A=[﹣2a,4a].
又∵(﹣1,1)A,
∴ ![]() ,解得
,解得 ![]() ,
,
∴实数a的取值范围是 ![]() .
.
【解析】(1)当a=1时,f(x)=x2﹣2x﹣8,不等式x2﹣2x﹣8≤0,化为(x﹣4)(x+2)≤0,解出即可.(2)由x2﹣2ax﹣8a2≤0,可得(x﹣4a)(x+2a)≤0,由于a>0,可得﹣2a≤x≤4a,即A=[﹣2a,4a].由于(﹣1,1)A,可得 ![]() ,解得即可.
,解得即可.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(2)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点?若过定点则求出该定点,若不存在则说明理由;
是否过定点?若过定点则求出该定点,若不存在则说明理由;
(3)若![]() 为圆
为圆![]() 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为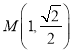 ,求四边形
,求四边形![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .现以
.现以![]() 为一边向外作正方形
为一边向外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使
翻折,使![]() 平面与平面
平面与平面![]() 垂直,
垂直, ![]() 为
为![]() 的中点,如图 2.
的中点,如图 2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知右焦点为F(c,0)的椭圆M: ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且椭圆M关于直线x=c对称的图形过坐标原点.
,且椭圆M关于直线x=c对称的图形过坐标原点.
(1)求椭圆M的方程;
(2)过点(4,0)且不垂直于y轴的直线与椭圆M交于P,Q两点,点Q关于x轴的对称原点为E,证明:直线PE与x轴的交点为F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为![]() 元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.若使租赁公司的月收益最大,每辆车的月租金应该定为__________.
元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.若使租赁公司的月收益最大,每辆车的月租金应该定为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )
)
(1)若![]() ,用“五点法”在给定的坐标系中,画出函数
,用“五点法”在给定的坐标系中,画出函数![]() 在[0,π]上的图象.
在[0,π]上的图象.

(2)若![]() 偶函数,求
偶函数,求![]()
(3)在(2)的前提下,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 在
在![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com