
【题目】(1)已知![]() ,用分析法证明:
,用分析法证明: ![]() ;
;
(2)已知![]() ,
, ![]() 且
且![]() ,用反证法证明:
,用反证法证明: ![]() 都大于零.
都大于零.
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=sin(2x+ ![]() ),下列命题: ①函数图象关于直线x=﹣
),下列命题: ①函数图象关于直线x=﹣ ![]() 对称;
对称;
②函数图象关于点( ![]() ,0)对称;
,0)对称;
③函数图象可看作是把y=sin2x的图象向左平移个 ![]() 单位而得到;
单位而得到;
④函数图象可看作是把y=sin(x+ ![]() )的图象上所有点的横坐标缩短到原来的
)的图象上所有点的横坐标缩短到原来的 ![]() 倍(纵坐标不变)而得到;其中正确的命题是 .
倍(纵坐标不变)而得到;其中正确的命题是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节来临,有农民工兄弟![]() 、
、![]() 、
、![]() 、
、![]() 四人各自通过互联网订购回家过年的火车票,若订票成功即可获得火车票,即他们获得火车票与否互不影响.若
四人各自通过互联网订购回家过年的火车票,若订票成功即可获得火车票,即他们获得火车票与否互不影响.若![]() 、
、![]() 、
、![]() 、
、![]() 获得火车票的概率分别是
获得火车票的概率分别是![]() ,其中
,其中![]() ,又
,又![]() 成等比数列,且
成等比数列,且![]() 、
、![]() 两人恰好有一人获得火车票的概率是
两人恰好有一人获得火车票的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 、
、![]() 是一家人且两人都获得火车票才一起回家,否则两人都不回家.设
是一家人且两人都获得火车票才一起回家,否则两人都不回家.设![]() 表示
表示![]() 、
、![]() 、
、![]() 、
、![]() 能够回家过年的人数,求
能够回家过年的人数,求![]() 的分布列和期望
的分布列和期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5)计算回归系数 ![]() ,
, ![]() .公式为
.公式为 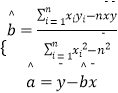 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点
,以极点为原点![]() ,极轴为
,极轴为![]() 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若用![]() 代换曲线
代换曲线![]() 的普通方程中的
的普通方程中的![]() 得到曲线
得到曲线![]() 的方程,若
的方程,若![]() 分别是曲线
分别是曲线![]() 和曲线
和曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com