
【题目】设![]() 、
、![]() 为双曲线
为双曲线![]() 上的两点,
上的两点,![]() 为线段
为线段![]() 的中点,线段
的中点,线段![]() 的垂直平分线与双曲线交于
的垂直平分线与双曲线交于![]() 、
、![]() 两点
两点
(1)确定![]() 的取值范围
的取值范围
(2)试判断![]() 、
、![]() 、
、![]() 、
、![]() 四点是否共圆?并说明理由
四点是否共圆?并说明理由
科目:高中数学 来源: 题型:
【题目】如图,长方体![]() 的长,宽,高分别为4,3,5,现有一甲壳虫从
的长,宽,高分别为4,3,5,现有一甲壳虫从![]() 点出发沿长方体表面爬行到
点出发沿长方体表面爬行到![]() 点来获取食物.
点来获取食物.
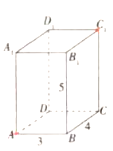
(1)甲壳虫想尽快获取食物可通过哪些路径获取?
(2)哪条获取食物的路径最短?最短为多少?
(3)此类问题的一般处理方法是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:


(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;

(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人.
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
![]()
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() (底面为正三角形,侧棱和底面垂直)的所有棱长都为2,
(底面为正三角形,侧棱和底面垂直)的所有棱长都为2,![]() 为
为![]() 的中点,O为
的中点,O为![]() 中点.
中点.
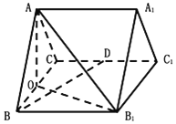
(1)求证:![]() 平面
平面![]() .
.
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接旅游旺季的到来,少林寺设置了一个专门安排旅客住宿的客栈,寺庙的工作人员发现为游客准备的食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会呈现周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在![]() 月份最少,在
月份最少,在![]() 月份最多,相差约
月份最多,相差约![]() 人;
人;
③![]() 月份入住客栈的游客约为
月份入住客栈的游客约为![]() 人,随后逐月增加直到
人,随后逐月增加直到![]() 月份达到最多.
月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问哪几个月份要准备![]() 份以上的食物?
份以上的食物?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,总存在实数
,总存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 关于参数
关于参数![]() 的不动点.
的不动点.
(1)当![]() ,
,![]() 时,求
时,求![]() 关于参数
关于参数![]() 的不动点;
的不动点;
(2)若对任意实数![]() ,函数
,函数![]() 恒有关于参数
恒有关于参数![]() 两个不动点,求
两个不动点,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() 时,函数
时,函数![]() 在
在![]() 上存在两个关于参数
上存在两个关于参数![]() 的不动点,试求参数
的不动点,试求参数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角![]() 和以
和以![]() 为直径的半圆拼接而成,点
为直径的半圆拼接而成,点![]() 为半圈上一点(异于
为半圈上一点(异于![]() ,
,![]() ),点
),点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,
,![]() ,设
,设![]() .
.

(1)为了使工艺礼品达到最佳观赏效果,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,工艺礼品达到最佳观赏效果;
为何值时,工艺礼品达到最佳观赏效果;
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,
为何值时,![]() 取得最大值,并求该最大值.
取得最大值,并求该最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 9 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)该小组发现种子的发芽数![]() (颗)与昼夜温差
(颗)与昼夜温差![]() (℃)呈线性相关关系,试求:线性回归方程
(℃)呈线性相关关系,试求:线性回归方程![]() .
.
(参考公式:线性回归方程![]() 中系数计算公式
中系数计算公式 ,
,![]() .其中
.其中![]() ,
,![]() 表示样本均值.
表示样本均值.
参考数据:![]() ;
;![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com