
分析 (1)f(x)=0有解,(a,b)应满足a2-4b≥0,确定基本事件的个数,利用概率公式,即可求f(x)=0有解的概率;
(2)若a、b都是从区间[0,4]任取的一个实数,以面积为测度,即可求f(1)>0成立的概率.
解答 解:(1)(a,b)的所有结果有36种,设“f(x)=0有解”为事件A,则
(a,b)应满足a2-4b≥0.这样的(a,b)有19个,即(2,1)、(3,1)、(3,2)、(4,1)、(4,2)、(4,3)、(4,4)、(5,1)(5,2)、(5,3)、(5,4)、(5,5)、(5.6)、(6,1)、(6,2)、(6,3)、(6,4)、(6,5)、(6,6).所以P(A)=$\frac{19}{36}$.…(6分)
(2)f(1)=-1+a-b>0,即a-b>1,如图: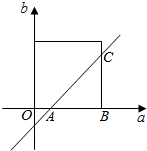
A(1,0),B(4,0),C(4,3),S△ABC=$\frac{9}{2}$,
P=$\frac{S△ABC}{S矩}$=$\frac{\f(9}{2},4×4)$=$\frac{9}{32}$.(12分)
点评 本题考查古典概型、几何概型概率的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,1)∪(1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1)∪(1,2) | B. | (-∞,0)∪(0,1)∪(1,2) | C. | (-∞,0)∪(1,2) | D. | (-∞,0)∪(0,1)∪(1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+2i | B. | 4-2i | C. | 2+4i | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com