
【题目】如图所示,A,B分别是椭圆C:![]() =1(a>b>0)的左右顶点,F为其右焦点,2是|AF|与|FB|的等差中项,
=1(a>b>0)的左右顶点,F为其右焦点,2是|AF|与|FB|的等差中项,![]() 是|AF|与|FB|的等比中项.点P是椭圆C上异于A,B的任一动点,过点A作直线l⊥x轴.以线段AF为直径的圆交直线AP于点A,M,连接FM交直线l于点Q.
是|AF|与|FB|的等比中项.点P是椭圆C上异于A,B的任一动点,过点A作直线l⊥x轴.以线段AF为直径的圆交直线AP于点A,M,连接FM交直线l于点Q.
(1)求椭圆C的方程;
(2)试问在x轴上是否存在一个定点N,使得直线PQ必过该定点N?若存在,求出点N的坐标,若不存在,说明理由.

【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据题意,用a、c表示出|AF|、|FB,再根据等差中项与等比中项定义求出a、b、c,进而求得椭圆方程。
(2)假设存在这样的定点。设出动点P,由P再椭圆上,用x0表示y0,再表示出FM的方程,联立FM与直线![]() ,得交点Q,进而求得过定点的坐标。
,得交点Q,进而求得过定点的坐标。
(1)由题意得|AF|=a+c,|FB|=a-c,
即![]()
解得a=2,c=1,∴b2=4-1=3.
∴所求椭圆的方程为![]() =1.
=1.
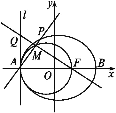
(2)假设在x轴上存在一个定点N(n,0),使得直线PQ必过定点N(n,0).
设动点P(x0,y0),由于P点异于A,B,故y0≠0,
由点P在椭圆上,故有![]() =1,
=1,
∴![]() . ①
. ①
又由(1)知A(-2,0),F(1,0),
∴直线AP的斜率kAP=![]() .
.
又点M是以线段AF为直径的圆与直线AP的交点,∴AP⊥FM.
∴kAP·kMF=-1kMF=-![]() =-
=-![]() .
.
∴直线FM的方程y=-![]() (x-1).
(x-1).
联立FM,l的方程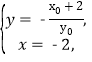
得交点Q![]() .
.
∴P,Q两点连线的斜率kPQ=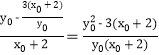 , ②
, ②
将①式代入②式,并整理得kPQ=![]() ,
,
又P,N两点连线的斜率kPN=![]() .
.
若直线QP必过定点N(n,0),则必有kPQ=kPN恒成立,即![]() ,
,
整理得4![]() =-3(x0+2)(x0-n), ③
=-3(x0+2)(x0-n), ③
将①式代入③式,得4×![]() =-3(x0+2)(x0-n),解得n=2,故直线PQ过定点(2,0).
=-3(x0+2)(x0-n),解得n=2,故直线PQ过定点(2,0).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex[ ![]() x3﹣2x2+(a+4)x﹣2a﹣4],其中a∈R,e为自然对数的底数.
x3﹣2x2+(a+4)x﹣2a﹣4],其中a∈R,e为自然对数的底数.
(1)若函数f(x)的图象在x=0处的切线与直线x+y=0垂直,求a的值;
(2)关于x的不等式f(x)<﹣ ![]() ex在(﹣∞,2)上恒成立,求a的取值范围;
ex在(﹣∞,2)上恒成立,求a的取值范围;
(3)讨论函数f(x)极值点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+be﹣x , (b∈R),函数g(x)=2asinx,(a∈R).
(1)求函数f(x)的单调区间;
(2)若b=﹣1,f(x)>g(x),x∈(0,π),求a取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知圆C的圆心C( ![]() ,
, ![]() ),半径r=
),半径r= ![]() .
.
(1)求圆C的极坐标方程;
(2)若α∈[0, ![]() ),直线l的参数方程为
),直线l的参数方程为 ![]() (t为参数),直线l交圆C于A、B两点,求弦长|AB|的取值范围.
(t为参数),直线l交圆C于A、B两点,求弦长|AB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图:
(1)若从甲、乙两名学生中选择1人参加该知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(2)若从学生甲的6次培训成绩中随机选择2个,记选到的分数超过87分的个数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,圆O的两弦AB和CD交于点E,作EF∥CB,并且交AD的延长线于点F,FG切圆O于点G.
(1)求证:△DEF∽△EFA;
(2)如果FG=1,求EF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2-6x+5≤0,q:x2-2x+1-m2≤0(m>0).
(1)若m=2,且p∧q为真,求实数x的取值范围;
(2)若p是q的充分不必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线C1的参数方程为  (θ为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,两坐标系取相同的单位长度,曲线C2的极坐标方程为ρ=﹣2sin(θ+
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,两坐标系取相同的单位长度,曲线C2的极坐标方程为ρ=﹣2sin(θ+ ![]() ).
).
(1)把曲线C1的参数方程化为极坐标方程;
(2)求曲线C1与C2的交点M(ρ1 , θ1)的极坐标,其中ρ1≤0,0≤θ1<2π.
查看答案和解析>>
科目:高中数学 来源: 题型:
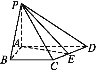
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
求证:CD⊥平面PAE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com