练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】不等式的解集为，则不等式的解集为（ ）

    A. B. C. D.

    【答案】A

    【解析】

    根据题意，分析可得方程（x+b）[（a﹣1）x+（1﹣b）]=0的两根为（﹣1）和3，则有，解可得a、b的值，进而可得不等式x2+bx﹣2a＜0即x2﹣3x﹣10＜0，解可得不等式的解集，即可得答案．

    根据题意，不等式（x+b）[（a﹣1）x+（1﹣b）]＞0的解集为（﹣∞，﹣1）∪（3，+∞），

    则方程（x+b）[（a﹣1）x+（1﹣b）]=0的两根为（﹣1）和3，

    则有，

    解可得：a=5，b=﹣3，

    则不等式x2+bx﹣2a＜0即x2﹣3x﹣10＜0，

    解可得：﹣2＜x＜5，

    即不等式x2+bx﹣2a＜0的解集为（﹣2，5）；

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某公司共有60位员工，为提高员工的业务技术水平，公司拟聘请专业培训机构进行培训．培训的总费用由两部分组成：一部分是给每位参加员工支付400元的培训材料费；另一部分是给培训机构缴纳的培训费．若参加培训的员工人数不超过30人，则每人收取培训费1000元；若参加培训的员工人数超过30人，则每超过1人，人均培训费减少20元．设公司参加培训的员工人数为x人，此次培训的总费用为y元．

    （1）求出y与x之间的函数关系式；

    （2）请你预算：公司此次培训的总费用最多需要多少元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l1：ax－by－1＝0(a、b不同时为0)，l2：(a＋2)x＋y＋a＝0.

    (1)若b＝0且l1⊥l2，求实数a的值；

    (2)当b＝2，且l1∥l2时，求直线l1与l2之间的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知指数函数y=g（x）满足：g（3）=8，定义域为R的函数f（x）= 是奇函数．

    （1）确定y=g（x），y=f（x）的解析式；

    （2）若h（x）=f（x）+a在（﹣1，1）上有零点，求a的取值范围；

    （3）若对任意的t∈（﹣4，4），不等式f（6t﹣3）+f（t2﹣k）＜0恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中， 平面， ， ， 是的中点， 是等腰三角形， 是的中点， 是上一点.

    （Ⅰ）若，证明： 平面；

    （Ⅱ）求直线与平面所成角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣2|．
    （1）解不等式：f（x+1）+f（x+2）＜4；
    （2）已知a＞2，求证：x∈R，f（ax）+af（x）＞2恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在Rt△AOB中， ，斜边AB=4，D是AB中点，现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥，点C为圆锥底面圆周上一点，且∠BOC=90°，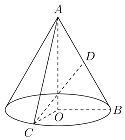
    （1）求圆锥的侧面积；
    （2）求直线CD与平面BOC所成的角的大小；（用反三角函数表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，过点作圆的切线，切点分别为．直线恰好经过的右顶点和上顶点．

    （1）求椭圆的方程；

    （2）如图，过椭圆的右焦点作两条互相垂直的弦， ．

    ①设中点分别为，证明：直线必过定点，并求此定点坐标；

    ②若直线， 的斜率均存在时，求由四点构成的四边形面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知， 是抛物线上两点，且与两点横坐标之和为3.

    (1)求直线的斜率；

    (2)若直线，直线与抛物线相切于点，且，求方程.

    查看答案和解析>>

    同步练习册答案