
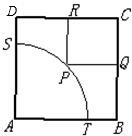
 如图,ABCD是一块边长为100m的正方形地皮,其中AST是半径为90m的扇形小山,其余部分都是平地,一开发商想在平地上建一个矩形的停车场,使矩形的一个顶点P在圆弧ST上,相邻两边CQ,CR落在正方形的BC,CD边上,求矩形停车场PQCR面积的最大值与最小值.
如图,ABCD是一块边长为100m的正方形地皮,其中AST是半径为90m的扇形小山,其余部分都是平地,一开发商想在平地上建一个矩形的停车场,使矩形的一个顶点P在圆弧ST上,相邻两边CQ,CR落在正方形的BC,CD边上,求矩形停车场PQCR面积的最大值与最小值. 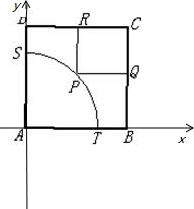 解:建立如图所示直角坐标系
解:建立如图所示直角坐标系| 2 |
| t2-1 |
| 2 |
| 10 |
| 9 |
| 2 |
| 2 |


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
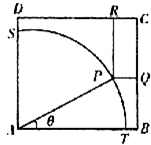 随着机动车数量的增加,对停车场所的需求越来越大,如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一座半径为90米的扇形小山,P是弧TS上一点,其余部分都是平地,现一开发商想在平地上建一个边落在BC和CD上的长方形停车场PQCR.
随着机动车数量的增加,对停车场所的需求越来越大,如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一座半径为90米的扇形小山,P是弧TS上一点,其余部分都是平地,现一开发商想在平地上建一个边落在BC和CD上的长方形停车场PQCR.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一半径为80米的扇形小山,P是弧TS上一点,其余部分都是平地.现一开发商想在平地上建造一个有边落在BC与CD上的长方形停车场PQCR.设∠PAT为θ,长方形停车场面积为S.
如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一半径为80米的扇形小山,P是弧TS上一点,其余部分都是平地.现一开发商想在平地上建造一个有边落在BC与CD上的长方形停车场PQCR.设∠PAT为θ,长方形停车场面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2004•黄埔区一模)如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一半径为90米的底面为扇形小山(P为
(2004•黄埔区一模)如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一半径为90米的底面为扇形小山(P为 | TS |
查看答案和解析>>
科目:高中数学 来源: 题型:
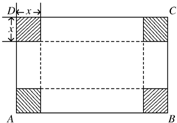 如图,ABCD是一块矩形铁板AB=48cm,BC=30cm,剪掉四个阴影部分的小正方形,沿虚线折叠后,焊接成一个无盖的长方体水箱.
如图,ABCD是一块矩形铁板AB=48cm,BC=30cm,剪掉四个阴影部分的小正方形,沿虚线折叠后,焊接成一个无盖的长方体水箱.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com