练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】甲、乙两位同学期末考试的语文、数学、英语、物理成绩如茎叶图所示，其中甲的一个数据记录模糊，无法辨认，用a来表示，已知两位同学期末考试四科的总分恰好相同，则甲同学四科成绩的中位数为（ ）

    A.92
    B.92.5
    C.93
    D.93.5

    【答案】C
    【解析】解：∵两位同学期末考试四科的总分恰好相同，

    ∴由茎叶图得87+90+94+95+a=89+85+96+98，

    即a=2，

    则甲的中位数为 =93，

    所以答案是：C

    【考点精析】通过灵活运用茎叶图，掌握茎叶图又称“枝叶图”，它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若函数 在 内任取两个实数p，q，且p≠q，不等式 恒成立，则a的取值范围是（ ）
    A.[﹣1，0]
    B.[﹣1，+∞）
    C.[0，3]
    D.[3，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知首项为1的正项数列{an}满足ak+1=ak+ai（i≤k，k=1，2，…，n﹣1），数列{an}的前n项和为Sn ．
    （1）比较ai与1的大小关系，并说明理由；
    （2）若数列{an}是等比数列，求 的值；
    （3）求证： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（cosx，sinx）， =（3，﹣ ），x∈[0，π]
    （1）若 ∥ ，求x的值；
    （2）记f（x）= ，求f（x）的最大值和最小值以及对应的x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a∈R，函数f（x）=log2（ +a）．
    （1）当a=5时，解不等式f（x）＞0；
    （2）若关于x的方程f（x）﹣log2[（a﹣4）x+2a﹣5]=0的解集中恰好有一个元素，求a的取值范围．
    （3）设a＞0，若对任意t∈[ ，1]，函数f（x）在区间[t，t+1]上的最大值与最小值的差不超过1，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足an+1=an﹣2anan+1 ， an≠0且a1=1．
    （1）求数列{an}的通项公式；
    （2）令 ，求数列{bn}的前2n项和T2n ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆O： （a＞b＞0）过点（ ，﹣ ），A（x0 ， y0）（x0y0≠0），其上顶点到直线 x+y+3=0的距离为2，过点A的直线l与x，y轴的交点分别为M、N，且 =2 ．
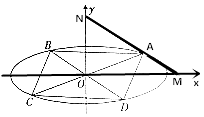
    （1）证明：|MN|为定值；
    （2）如图所示，若A，C关于原点对称，B，D关于原点对称，且 =λ ，求四边形ABCD面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了适应市场需要，某地准备建一个圆形生猪储备基地(如右图)，它的附近有一条公路，从基地中心O处向东走1 km是储备基地的边界上的点A ， 接着向东再走7 km到达公路上的点B；从基地中心O向正北走8 km到达公路的另一点C.现准备在储备基地的边界上选一点D ， 修建一条由D通往公路BC的专用线DE ， 求DE的最短距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}满足：a1=1，an+1+（﹣1）nan=2n﹣1．
    （1）求a2 ， a4 ， a6；
    （2）设bn=a2n ， 求数列{bn}的通项公式；
    （3）设Sn为数列{an}的前n项和，求S2018 ．

    查看答案和解析>>

    同步练习册答案