
【题目】进入12月以业,在华北地区连续出现两次重污染天气的严峻形势下,我省坚持保民生,保蓝天,各地严格落实机动车限行等一系列“管控令”,某市交通管理部门为了了解市民对“单双号限行”的态度,随机采访了200名市民,将他们的意见和是否拥有私家车的情况进行了统计,得到如下的![]() 列联表:
列联表:
赞同限行 | 不赞同限行 | 合计 | |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断能否在犯错误的概率不超过![]() 的前提下认为“对限行的态度与是否拥有私家车有关”;
的前提下认为“对限行的态度与是否拥有私家车有关”;
(2)为了了解限行之后是否对交通拥堵、环境染污起到改善作用,从上述调查的不赞同限行的人员中按是否拥有私家车分层抽样抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少有1人没有私家车的概率.
附: 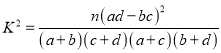 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)在犯错误概率不超过![]() 的前提下,不能认为“对限行的态度与是否拥有私家车”有关;(2)0.8.
的前提下,不能认为“对限行的态度与是否拥有私家车”有关;(2)0.8.
【解析】试题分析:(1)先根据卡方公式求![]() ,再与参考数据比较大小,作出判断,(2)先根据分层抽样确定没有私家车的2人,有私家车的4人,再根据枚举法确定从这6人中随机抽出3名总事件数,从中确定3人中至少有1人没有私家车的事件数,最后根据古典概型概率公式求概率.
,再与参考数据比较大小,作出判断,(2)先根据分层抽样确定没有私家车的2人,有私家车的4人,再根据枚举法确定从这6人中随机抽出3名总事件数,从中确定3人中至少有1人没有私家车的事件数,最后根据古典概型概率公式求概率.
试题解析:(1) ![]() .
.
所以在犯错误概率不超过![]() 的前提下,不能认为“对限行的态度与是否拥有私家车”有关.
的前提下,不能认为“对限行的态度与是否拥有私家车”有关.
(2)设从没有私家车的人中抽取![]() 人,从有私家车的人中抽取
人,从有私家车的人中抽取![]() 人,
人,
由分层抽样的定义可知![]() ,解得
,解得![]() ,
,
在抽取的6人中,没有私家车的2人记为![]() ,有私家车的4人记为
,有私家车的4人记为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则所有的基本事件如下:
,则所有的基本事件如下:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() 共20种.
共20种.
其中至少有1人没有私家车的情况有16种.
记事件![]() 为“至少有1人没有私家车”,则
为“至少有1人没有私家车”,则![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,某地有南北街道5条,东西街道5条,现在甲、乙、丙3名邮递员从该地西南角的邮局![]() 出发,送信到东北角的
出发,送信到东北角的![]() 地,要求所走路程最短,设图中点
地,要求所走路程最短,设图中点![]() ,
,![]() ,
,![]() 是交叉路口,且
是交叉路口,且![]() 路段由于修路不能通行.
路段由于修路不能通行.
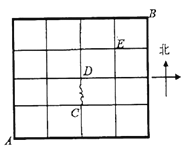
(1)求甲从![]() 到
到![]() 共有多少种走法?(用数字作答)
共有多少种走法?(用数字作答)
(2)求甲经过点![]() 的概率;
的概率;
(3)设3名邮递员恰有![]() 名邮递员经过点
名邮递员经过点![]() ,求随机变量
,求随机变量![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装批发市场1-5月份的服装销售量![]() 与利润
与利润![]() 的统计数据如下表:
的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销售量 | 3 | 6 | 4 | 7 | 8 |
利润 | 19 | 34 | 26 | 41 | 46 |
(1)从这五个月的利润中任选2个,分别记为![]() ,
, ![]() ,求事件“
,求事件“![]() ,
, ![]() 均不小于30”的概率;
均不小于30”的概率;
(2)已知销售量![]() 与利润
与利润![]() 大致满足线性相关关系,请根据前4个月的数据,求出
大致满足线性相关关系,请根据前4个月的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的利润的估计数据与真实数据的误差不超过2万元,则认为得到的利润的估计数据是理想的.请用表格中第5个月的数据检验由(2)中回归方程所得的第5个月的利润的估计数据是否理想.参考公式:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下面类比推理:
①“若2a<2b,则a<b”类比推出“若a2<b2,则a<b”;
②“(a+b)c=ac+bc(c≠0)”类比推出“![]() (c≠0)”;
(c≠0)”;
③“a,b∈R,若a-b=0,则a=b”类比推出“a,b∈C,若a-b=0,则a=b”;
④“a,b∈R,若a-b>0,则a>b”类比推出“a,b∈C,若a-b>0,则a>b(C为复数集)”.
其中结论正确的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若![]() 是
是![]() 的两个不同零点,是否存在实数
的两个不同零点,是否存在实数![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)设![]() ,函数
,函数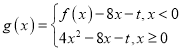 ,存在
,存在![]() 个零点.
个零点.
(i)求![]() 的取值范围;
的取值范围;
(ii)设![]() 分别是这
分别是这![]() 个零点中的最小值与最大值,求
个零点中的最小值与最大值,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以“你我中国梦,全民建小康”为主题“社会主义核心价值观”为主线,为了解![]() 、
、![]() 两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度,对
两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度,对![]() 、
、![]() 地区的
地区的![]() 名观众进行统计,统计结果如下:
名观众进行统计,统计结果如下:
非常满意 | 满意 | 合计 | |
|
|
| |
|
|
| |
合计 |
在被调查的全体观众中随机抽取![]() 名“非常满意”的人是
名“非常满意”的人是![]() 地区的概率为
地区的概率为![]() ,且
,且![]() .
.
(1)现从![]() 名观众中用分层抽样的方法抽取
名观众中用分层抽样的方法抽取![]() 名进行问卷调查,则应抽取“满意”的
名进行问卷调查,则应抽取“满意”的![]() 、
、![]() 地区的人数各是多少?
地区的人数各是多少?
(2)在(1)抽取的“满意”的观众中,随机选出![]() 人进行座谈,求至少有两名是
人进行座谈,求至少有两名是![]() 地区观众的概率?
地区观众的概率?
(3)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系?
的把握认为观众的满意程度与所在地区有关系?
附:
|
|
|
|
|
|
|
|
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 在椭圆
在椭圆![]() :
:![]() 上.若点
上.若点![]() ,
,![]() ,且
,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)设椭圆![]() 的焦距为4,
的焦距为4,![]() ,
,![]() 是椭圆
是椭圆![]() 上不同的两点,线段
上不同的两点,线段![]() 的垂直平分线为直线
的垂直平分线为直线![]() ,且直线
,且直线![]() 不与
不与![]() 轴重合.
轴重合.
①若点![]() ,直线
,直线![]() 过点
过点![]() ,求直线
,求直线![]() 的方程;
的方程;
② 若直线![]() 过点
过点![]() ,且与
,且与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() 点横坐标的取值范围.
点横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,新街口某新开业的商场在过去一个月内(以30天计),顾客人数![]() (千人)与时间
(千人)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]() (
(![]() ),人均消费
),人均消费![]() (元)与时间
(元)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]()
(1)求该商场的日收益![]() (千元)与时间
(千元)与时间![]() (天)(
(天)(![]() ,
, ![]() )的函数关系式;
)的函数关系式;
(2)求该商场日收益的最小值(千元).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com