[题目]已知顶点在单位圆上的中.角的对边分别为 .且 .(1)求的值,(2)若 .求的面积. 题目和参考答案——青夏教育精英家教网—

【题目】已知顶点在单位圆上的中，角的对边分别为，且 .
（1）求的值；
（2）若，求的面积.

【答案】
（1）解：因为，
所以，
所以 .
因为，所以，
所以 .
因为，所以 .
所以 .
故答案为： .
（2）解：据（1）求解知，又，∴ ，
又据题设知，得 .
因为由余弦定理，得，
所以 .
所以
故答案为： S Δ A B C=
【解析】（1）先用正弦定理将边角关系转化为角的关系，再用两角和的正弦公式得到关于角A的关系式，求cosA;
（2）先用条件求出a边，再用余弦定理求bc，再求面积.
【考点精析】掌握两角和与差的正弦公式是解答本题的根本，需要知道两角和与差的正弦公式：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=（x﹣2）ex﹣ +kx（k是常数，e是自然对数的底数，e=2.71828…）在区间（0，2）内存在两个极值点，则实数k的取值范围是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知以点为圆心的圆过点和，线段的垂直平分线交圆于点、，且,

（1）求直线的方程；（2）求圆的方程。

（3）设点在圆上，试探究使的面积为 8 的点共有几个？证明你的结论

查看答案和解析>>

科目：高中数学 来源： 题型：

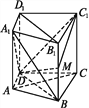
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.

(1)求证:B1D1∥平面A1BD;

(2)求证:MD⊥AC;

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数在区间上有1个零点；函数图象与轴交于不同的两点.若“ ”是假命题，“ ”是真命题，求实数的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）

	参加书法社团	未参加书法社团
参加演讲社团	8	5
未参加书法社团	2	30

（1）从该班随机选 1 名同学，求该同学至少参加上述一个社团的概率；

（2）在既参加书法社团又参加演讲社团的 8 名同学中，有 5 名男同学,3名女同学.现从这 5 名男同学和 3 名女同学中各随机选 1 人，求被选中且未被选中的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】祖暅原理：“幂势既同，则积不容异”，它是中国古代一个涉及几何体体积问题，意思是两个等高的几何体，如在同高处的截面积恒相等，则体积相等，设A，B为两个等高的几何体，p：A,B的体积相等，q：A,B在同高处的截面积不恒相等，根据祖暅原理可知，q是-p的（）
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】定义域为的函数满足：，且对于任意实数，恒有，当时，.