分析:先画出约束条件的可行域,根据
(1)z=2x+y即y=-2x+z,z表示直线的纵截距;
(2)z=x
2+y
2所表示的几何意义:点到原点距离的平方;
(3)
z=的几何意义是图中阴影部分中的点与原点连线的斜率,分析图形找出满足条件的点,即可得到结论.
解答:解:满足约束条件的可行域
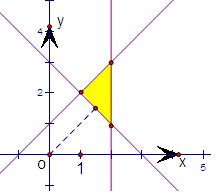
如图所示,三角形三个顶点的坐标分别为(2,1),(2,3),(1,2)
(1)z=2x+y即y=-2x+z,z表示直线的纵截距,则z=2x+y在(2,3)处取得最大值为7,在(1,2)处取得最小值为4;
(2)∵z=x
2+y
2所表示的几何意义为:点到原点距离的平方
由图可得,原点到图中阴影部分中的直线x+y-3=0的距离的平方时,
此时z=x
2+y
2的最小,最小值为
()2=
,点(2,3)到原点的距离最大,最大值为13;
(3)
z=的几何意义是图中阴影部分中的点与原点连线的斜率,在点(2,1)处,斜率取得最小值为
;在(1,2)处,斜率取得最大值为2.
点评:本题考查线性规划问题,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.



