
分析 (1)把点(1,0)代入函数解析式,求出a的值即得f(x)的解析式;
(2)化简函数g(x),把g(x)-k≤0在x∈[e-1,e2]上恒成立转化为求g(x)在x∈[e-1,e2]上的最大值问题,从而求出k的取值范围;
(3)化简函数h(x),讨论m的取值,求出h(x)在区间(-$\frac{3}{2}$,2]上有零点时m的取值范围.
解答 解:(1)∵函数f(x)=logax+a-e过点(1,0),
∴f(1)=a-e=0,
解得a=e,
∴函数f(x)=lnx;
(2)∵g(x)-k≤0在x∈[e-1,e2]上恒成立,
即k≥g(x)max;
函数g(x)=f2(x)-2f(e2x)+3
=ln2x-2ln(e2x)+3
=ln2x-2lnx-1
=(lnx-1)2-2,
令t=lnx,∵x∈[e-1,e2],
∴t∈[-1,2],∴y=(t-1)2-2,
当t=-1时,y取得最大值2,
即g(x)max=2,
∴k的取值范围是k≥2;
(3)【解法一】∵函数h(x)=af(x+1)+mx2-3m+1
=eln(x+1)+mx2-3m+1
=(x+1)+mx2-3m+1,其中x>-1;
由h(x)=0,得m=-$\frac{x+2}{{x}^{2}-3}$(x≠±$\sqrt{3}$且-$\frac{3}{2}$<x≤2);
∴m=-$\frac{x+2}{{(x+2)}^{2}-4(x+2)+1}$,
令u=x+2($\frac{1}{2}$<u≤4且u≠2±$\sqrt{3}$),
则m=-$\frac{u}{{u}^{2}-4u+1}$=-$\frac{1}{u+\frac{1}{u}-4}$;
令p(u)=u+$\frac{1}{u}$,当$\frac{1}{2}$<u<1时,p(u)是减函数,
当1<u≤4时,p(u)是增函数;
且p($\frac{1}{2}$)=$\frac{5}{2}$,p(1)=2,p(4)=$\frac{17}{4}$,
∴2≤p(u)≤$\frac{17}{4}$且p(u)≠4,
∴0<4-p(u)≤2或-$\frac{1}{4}$≤4-p(u)<0,
∴m的取值范围是m≥$\frac{1}{2}$或m≤-4.
【解法二】;函数h(x)=af(x+1)+mx2-3m+1
=eln(x+1)+mx2-3m+1
=(x+1)+mx2-3m+1,其中x∈(-$\frac{3}{2}$,2];
当m=0时,h(x)=x+2的零点是-2,不满足题意;
当m≠0时,若h(x)=x+1+mx2-3m+1在(-$\frac{3}{2}$,2]上有二重零点,
则△=1-4m(2-3m)=0,解得m=$\frac{1}{2}$或$\frac{1}{6}$,
此时x1=x2=-$\frac{1}{2m}$∈(-$\frac{3}{2}$,2],∴m=$\frac{1}{2}$;
若h(x)=x+1+mx2-3m+1在(-$\frac{3}{2}$,2]上只有一个零点且不是二重零点,
则h(-$\frac{3}{2}$)•h(1)≤0,解得m≤-4或m≥$\frac{2}{3}$,
验证m=-4和m=$\frac{2}{3}$时,h(x)在(-$\frac{3}{2}$,2]上都有零点,∴m≤-4或m≥$\frac{2}{3}$;
若h(x)=x+1+mx2-3m+1在(-$\frac{3}{2}$,2]上有二个相异零点时,
则$\left\{\begin{array}{l}{m>0}\\{△>0}\\{-\frac{3}{2}<-\frac{1}{2m}<2}\\{h(2)≥0}\\{h(-\frac{3}{2})>0}\end{array}\right.$或$\left\{\begin{array}{l}{m<0}\\{△>0}\\{-\frac{3}{2}<-\frac{1}{2m}<2}\\{h(2)≤0}\\{h(-\frac{3}{2})<0}\end{array}\right.$,解得$\frac{1}{2}$<m<$\frac{2}{3}$,
综上,m的取值范围是m≤-4或m≥$\frac{1}{2}$.
点评 本题考查了对数函数的图象与性质的应用问题,也考查了复合函数的性质与应用问题,考查了不等式的解法与应用问题,零点的判断问题,同时也考查了分类讨论的数学思想,是综合性题目.


科目:高中数学 来源: 题型:解答题
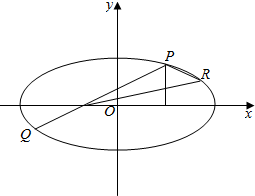 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦点为F1、F2,过F2作垂直于x轴的直线交椭圆于P点(点P在x轴上方),连结PF1并延长交椭圆于另一点Q.设$\overrightarrow{P{F_1}}=λ\overrightarrow{{F_1}Q}$(2≤λ≤$\frac{7}{3}$).
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦点为F1、F2,过F2作垂直于x轴的直线交椭圆于P点(点P在x轴上方),连结PF1并延长交椭圆于另一点Q.设$\overrightarrow{P{F_1}}=λ\overrightarrow{{F_1}Q}$(2≤λ≤$\frac{7}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$+1 | B. | $\sqrt{2}$+1 | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com