
【题目】已知定义在R上的函数![]() 是奇函数.
是奇函数.
(1)求实数a,b的值;
(2)若对任意实数x,不等式f(4x﹣k2x)+f(22x+1﹣k)<0恒成立,求实数k的取值范围.
【答案】(1)a=2,b=1(2)(﹣∞,0]
【解析】
(1)根据奇函数的必要条件,利用![]() ,求出
,求出![]() 值,再用奇函数的定义证明;
值,再用奇函数的定义证明;
(2)![]() 恒成立,由已知转化为
恒成立,由已知转化为![]()
恒成立,利用![]() 在
在![]() 单调递减,原不等式转为
单调递减,原不等式转为![]() 恒成立,换元令
恒成立,换元令![]() ,转化为
,转化为![]() 恒成立,设
恒成立,设![]() ,只需求出
,只需求出![]() ,即可求出结论.
,即可求出结论.
定义在R上的函数![]() 是奇函数,
是奇函数,
由.f(0)=0,可得b=1.
由f(﹣1)=﹣f(1),即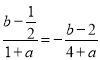 ,
,
解得a=2.∴f(x)![]() ,
,
![]() .
.
故得实数a=2,b=1.
(2)由![]() ,
,
∵y=2x+1在![]() 上单调递增且
上单调递增且![]() ,∴f(x)在
,∴f(x)在![]() 上单调递减;
上单调递减;
那么不等式f(4x﹣k2x)<﹣f(22x+1﹣k)恒成立,
∵f(x)是奇函数,又是递减函数;
则![]() ,
,
可得![]() 恒成立,
恒成立,
令t=2x,(t>0)
则![]() 恒成立,
恒成立,
若![]() ,则
,则![]() ,可得
,可得![]() 成立;
成立;
若![]() ,则
,则![]() ,即
,即![]() ,此时无解
,此时无解
综上实数k的取值范围![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ax-![]() x2-3ln x,其中a∈R,为常数.
x2-3ln x,其中a∈R,为常数.
(1)若f(x)在x∈[1,+∞)上是减函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)在x∈[1,a]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知倾斜角为
中,已知倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)写出曲线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 有两个不同的交点
有两个不同的交点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵![]() 与刍童
与刍童![]() 的组合体中
的组合体中![]() ,
,![]() . 台体体积公式:
. 台体体积公式: ![]() , 其中
, 其中![]() 分别为台体上、下底面面积,
分别为台体上、下底面面积, ![]() 为台体高.
为台体高.
(1)证明:直线![]()
![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
, ![]() ,三棱锥
,三棱锥![]() 的体积
的体积![]() ,求 该组合体的体积.
,求 该组合体的体积. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,已知an>0,an2+2an=4Sn+3.
(1)求a1的值;
(2)求{an}的通项公式:
(3)设bn=![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高二年级期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段![]() ,
,![]() ,……,
,……,![]() 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:

(1)求出物理成绩低于50分的学生人数;
(2)估计这次考试物理学科及格率(60分以上为及格);
(3)从物理成绩不及格的学生中选x人,其中恰有一位成绩不低于50分的概率为![]() ,求此时x的值;
,求此时x的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 在
在![]() 处取极大值,在
处取极大值,在![]() 处取极小值.
处取极小值.
(1)若![]() ,求函数
,求函数![]() 的单调区间和零点个数;
的单调区间和零点个数;
(2)在方程![]() 的解中,较大的一个记为
的解中,较大的一个记为![]() ;在方程
;在方程![]() 的解中,较小的一个记为
的解中,较小的一个记为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)证明:当![]() 时,
时,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com