
【题目】如图,四棱锥![]() 的底面是正方形,
的底面是正方形, ![]() 平面
平面![]() ,
,![]() ,点
,点![]() 是
是![]() 上的点,且
上的点,且![]() .
.

(1)求证:对任意的![]() ,都有
,都有![]() .
.
(2)设二面角C-AE-D的大小为![]() ,直线BE与平面
,直线BE与平面![]() 所成的角为
所成的角为![]() ,
,
若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)因为SD⊥平面ABCD,BD是BE在平面ABCD上的射影,由三垂线定理只要证AC
⊥BD即可.(2)先找出θ计算出cosθ,再找到![]() ,求出点O到BE的距离,再求出sin
,求出点O到BE的距离,再求出sin![]() ,解
,解
方程![]() 得到
得到![]() 的值.
的值.
(1)证明:连接BE、BD,由底面ABCD是正方形可得AC⊥BD.
∵SD⊥平面ABCD,∴BD是BE在平面ABCD上的射影,∴AC⊥BE
(2)解:由SD⊥平面ABCD知,∠DBE=φ,
∵SD⊥平面ABCD,CD平面ABCD,∴SD⊥CD.
又底面ABCD是正方形,∴CD⊥AD,而SD∩AD=D,CD⊥平面SAD.
连接AE、CE,过点D在平面SAD内作DF⊥AE于F,连接CF,则CF⊥AE,
故∠CFD是二面角C﹣AE﹣D的平面角,即∠CFD=θ.
在Rt△ADE中,∵AD=![]() a,DE=λa∴AE=a
a,DE=λa∴AE=a![]()
从而DF=![]() =
=![]()
在Rt△CDF中,tanθ=![]() =
=![]() ,所以
,所以![]() .
.
过点B作EO的垂线BG,因为AC⊥平面BDE,所以AC⊥BG,
所以∠BEO就是直线BE与平面![]() 所成的角
所成的角![]() ,
,
设点O到BE的距离为h,则由等面积得![]()
所以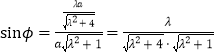 ,
,
因为![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax﹣a﹣x+2,若g(2)=a,则f(2)=( )
A.2
B.![]()
C.![]()
D.a2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们休闲方式的一次调查中,其中主要休闲方式的选择有看电视和运动,现共调查了100人,已知在这100人中随机抽取1人,抽到主要休闲方式为看电视的人的概率为![]() 。
。
(1)完成下列2×2列联表;
休闲方式为看电视 | 休闲方式为运动 | 合计 | |
女性 | 40 | ||
男性 | 30 | ||
合计 |
(2)请判断是否可以在犯错误的概率不超过0.005的前提下认为性别与休闲方式有关系?
参考公式![]()
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.025 | 0.010 | 0.005 |
k | 1.323 | 2.072 | 2.706 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了整顿食品的安全卫生,食品监督部门对某食品厂生产的甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克) 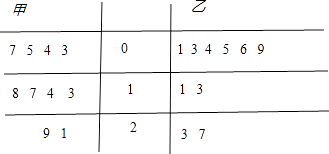
规定:当食品中的有害微量元素含量在[0,10]时为一等品,在(10,20]为二等品,20以上为劣质品.
(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个.求甲的一等品数与乙的一等品数相等的概率;
(2)每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元.根据上表统计得到的甲、乙两种食品为一等品、二等品、劣质品,的频率分别估计这两种食品为,一等品、二等品、劣质品的概率.若分别从甲、乙食品中各抽取l件,设这两件食品给该厂带来的盈利为X,求随机变量X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣mx(m∈R).
(1)讨论函数f(x)的单调区间;
(2)当m≥ ![]() 时,设g(x)=2f(x)+x2的两个极值点x1 , x2(x1<x2)恰为h(x)=lnx﹣cx2﹣bx的零点,求y=(x1﹣x2)h′(
时,设g(x)=2f(x)+x2的两个极值点x1 , x2(x1<x2)恰为h(x)=lnx﹣cx2﹣bx的零点,求y=(x1﹣x2)h′( ![]() )的最小值.
)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,AB=3,BC=4,E,F分别在线段BC,AD上,EF∥AB,将矩形ABEF沿EF折起,记折起后的矩形为MNEF,且平面MNEF⊥平面ECDF.
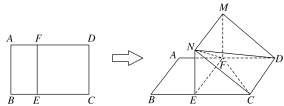
(1)在线段BC是否存在一点E,使得ND⊥FC ,若存在,求出EC的长并证明;
若不存在,请说明理由.
(2)求四面体NEFD体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCDA1B1C1D1中,O为底面ABCD的中心,P,Q分别为![]() 的中点.
的中点.
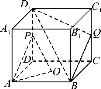
求证:(1)平面D1 BQ∥平面PAO.
(2)求异面直线QD1与AO所成角的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( ) 
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差小于乙的成绩的极差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设B、C是定点,且均不在平面α上,动点A在平面α上,且sin∠ABC=![]() , 则点A的轨迹为( )
, 则点A的轨迹为( )
A.圆或椭圆
B.抛物线或双曲线
C.椭圆或双曲线
D.以上均有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com