
【题目】已知函数f(x)= ![]() 为偶函数
为偶函数
(1)求实数a的值;
系;
(2)记集合E={y|y=f(x),x∈{﹣1,1,2}},λ=lg22+lg2lg5+lg5﹣ ![]() ,判断λ与E的
,判断λ与E的
(3)当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.
](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.
【答案】
(1)解:∵函数 ![]() 为偶函数.
为偶函数.
∴f(﹣x)=f(x)
即 ![]() =
= ![]()
∴2(a+1)x=0,
∵x为非零实数,
∴a+1=0,即a=﹣1
(2)解:由(1)得 ![]()
∴E={y|y=f(x),x∈{﹣1,1,2}}={0, ![]() }
}
而 ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]()
∴λ∈E
(3)解:∵ ![]() >0恒成立
>0恒成立
∴ ![]() 在
在 ![]() 上为增函数
上为增函数
又∵函数f(x)的值域为[2﹣3m,2﹣3n],
∴f( ![]() )=1﹣m2=2﹣3m,且f(
)=1﹣m2=2﹣3m,且f( ![]() )=1﹣n2=2﹣3n,
)=1﹣n2=2﹣3n,
又∵ ![]() ,m>0,n>0
,m>0,n>0
∴m>n>0
解得m= ![]() ,n=
,n= ![]()
【解析】(1)根据函数 ![]() 为偶函数f(﹣x)=f(x),构造关于a的方程组,可得a值;(2)由(1)中函数f(x)的解析式,将x∈{﹣1,1,2}代入求出集合E,利用对数的运算性质求出λ,进而根据元素与集合的关系可得答案(3)求出函数f(x)的导函数,判断函数的单调性,进而根据函数f(x)的值域为[2﹣3m,2﹣3n],x∈
为偶函数f(﹣x)=f(x),构造关于a的方程组,可得a值;(2)由(1)中函数f(x)的解析式,将x∈{﹣1,1,2}代入求出集合E,利用对数的运算性质求出λ,进而根据元素与集合的关系可得答案(3)求出函数f(x)的导函数,判断函数的单调性,进而根据函数f(x)的值域为[2﹣3m,2﹣3n],x∈ ![]() ,m>0,n>0构造关于m,n的方程组,进而得到m,n的值.
,m>0,n>0构造关于m,n的方程组,进而得到m,n的值.
【考点精析】解答此题的关键在于理解奇偶性与单调性的综合的相关知识,掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性,以及对利用导数研究函数的单调性的理解,了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
A.若l⊥m,mα,则l⊥α
B.若l⊥α,l∥m,则m⊥α
C.若l∥α,mα,则l∥m
D.若l∥α,m∥α,则l∥m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(Ⅰ)求图中a的值;
(Ⅱ)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(Ⅲ)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
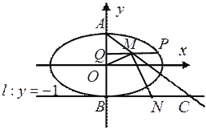
【题目】如图,已知中心在原点,焦点在![]() 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为![]() ,
, 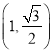 是椭圆上的一个点.
是椭圆上的一个点.
(1)求椭圆的标准方程;
(2)设椭圆的上、下顶点分别为![]() ,
, ![]() (
(![]() )是椭圆上异于
)是椭圆上异于![]() 的任意一点,
的任意一点, ![]() 轴,
轴, ![]() 为垂足,
为垂足, ![]() 为线段
为线段![]() 中点,直线
中点,直线![]() 交直线
交直线![]() 于点
于点![]() ,
, ![]() 为线段
为线段![]() 的中点,如果
的中点,如果![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+1)= ![]() ,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx2﹣mx﹣1.
(1)若对于x∈R,f(x)<0恒成立,求实数m的取值范围;
(2)若对于x∈[1,3],f(x)<5﹣m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将直线2x﹣y+λ=0沿x轴向左平移1个单位,所得直线与圆x2+y2+2x﹣4y=0相切,则实数λ的值为( )
A.﹣3或7
B.﹣2或8
C.0或10
D.1或11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn= ![]() ,n∈N* .
,n∈N* .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() +(﹣1)nan , 求数列{bn}的前2n项和.
+(﹣1)nan , 求数列{bn}的前2n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com