
| A. | [1,2) | B. | [$\frac{4}{3}$,2] | C. | ($\frac{4}{3}$,2) | D. | [$\frac{4}{3}$,2) |
分析 根据题中的条件得到函数的解析式为:当x∈(1,2]时,f(x)=(2-x)2;f(x)=2(2-$\frac{x}{2}$)2,x∈(2,4],f(x)=4(2-$\frac{x}{4}$)2,x∈(4,8],…,又y=k(x-1)的函数图象是过定点(1,0)的直线,再结合函数的图象根据题意求出参数的范围即可.
解答 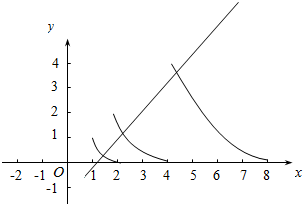 解:因为对任意的x∈(1,+∞)恒有f(2x)=2f(x)成立,
解:因为对任意的x∈(1,+∞)恒有f(2x)=2f(x)成立,
且当x∈(1,2]时,f(x)=(2-x)2;
f(x)=2(2-$\frac{x}{2}$)2,x∈(2,4],
f(x)=4(2-$\frac{x}{4}$)2,x∈(4,8],
…
由题意得y=k(x-1)的函数图象
是过定点P(1,0)的直线,
其中A(2,2),B(4,4),
如图所示直线与线段AB相交即可
(可以与B点重合但不能与A点重合),
kPA=$\frac{2-0}{2-1}$=2,kPB=$\frac{4-0}{4-1}$=$\frac{4}{3}$,
所以可得k的范围为$\frac{4}{3}$≤x<2.
故选:D.
点评 解决此类问题的关键是熟悉求函数解析式的方法以及函数的图象与函数的性质,数形结合思想是高中数学的一个重要数学数学,是解决数学问题的必备的解题工具.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com