
【题目】已知函数![]()
(1)求证:函数f(x)-g(x)必有零点;
(2)设函数G(x)=f(x)-g(x)-1
①若函数G(x)有两相异零点且![]() 在
在![]() 上是减函数,求实数m的取值范围。
上是减函数,求实数m的取值范围。
②是否存在整数a,b使得![]() 的解集恰好为
的解集恰好为![]() 若存在,求出a,b的值,若不存在,请说明理由。
若存在,求出a,b的值,若不存在,请说明理由。
【答案】(1)详见解析;(2)①(﹣∞,0]∪[2,+∞);②![]() 或
或![]() .
.
【解析】
(1)判断对应方程的△与0的关系,易得结论;
(2)由函数f(x)=mx+3,g(x)=x2+2x+m,我们易给出函数G(x)=f(x)﹣g(x)﹣1,①若|G(x)|在[﹣1,0]上是减函数,根据对折变换函数图象的特征,我们分△≤0和△>0两种情况进行讨论,可得到满足条件的m的取值范围;②若a≤G(x)≤b的解集恰好是[a,b],则 将a,b代入消去m,可以求出a,b的值.
将a,b代入消去m,可以求出a,b的值.
证明:(1)f(x)﹣g(x)=﹣x2+(m﹣2)x+3﹣m.
令f(x)﹣g(x)=0.
则△=(m﹣2)2﹣4(m﹣3)=m2﹣8m+16=(m﹣4)2≥0恒成立.
所以方程f(x)﹣g(x)=0有解.
所以函数f(x)﹣g(x)必有零点.
(2)①G(x)=f(x)﹣g(x)﹣1=﹣x2+(m﹣2)x+2﹣m.
①令G(x)=0,△=(m﹣2)2﹣4(m﹣2)=(m﹣2)(m﹣6).
当△≤0,即2≤m≤6时,G(x)=﹣x2+(m﹣2)x+2﹣m≤0恒成立,
所以|G(x)|=x2﹣(m﹣2)x+m﹣2.
因为|G(x)|在[﹣1,0]上是减函数,所以![]() 0.解得m≥2.
0.解得m≥2.
所以2≤m≤6.
当△>0,即m<2或m>6时,|G(x)|=|x2﹣(m﹣2)x+m﹣2|.
因为|G(x)|在[﹣1,0]上是减函数,
所以方程x2﹣(m﹣2)x+m﹣2=0的两根均大于零或一根大于零另一根小于零
且x![]() 1.
1.
所以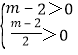 或
或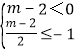
解得m>2或m≤0.
所以m≤0或m>6.
综上可得,实数m的取值范围为(﹣∞,0]∪[2,+∞).
②因为a≤G(x)≤b的解集恰好是[a,b],
所以![]()
由![]()
消去m,得ab﹣2a﹣b=0,显然b≠2.
所以a![]() 1
1![]() .
.
因为a,b均为整数,所以b﹣2=±1或b﹣2=±2.
解得或
![]() 或
或![]() 或
或![]() 因为a<b,且a
因为a<b,且a![]() b
b
所以![]() 或
或![]()


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】经销商小王对其所经营的某一型号二手汽车的使用年数![]() (0<
(0<![]() ≤10)与销售价格
≤10)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(附:回归方程![]() 中,
中,
(Ⅱ)已知每辆该型号汽车的收购价格为![]() 万元,根据(Ⅰ)中所求的回归方程,
万元,根据(Ⅰ)中所求的回归方程,
预测![]() 为何值时,小王销售一辆该型号汽车所获得的利润
为何值时,小王销售一辆该型号汽车所获得的利润![]() 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】. (12分)如图所示,函数![]() 的一段图象过点
的一段图象过点![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得函数
个单位,得函数![]() 的图象,求函数
的图象,求函数![]() 的最大值,并求此时自变量
的最大值,并求此时自变量![]() 的取值集合.
的取值集合.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①直线l的方向向量为![]() =(1,﹣1,2),直线m的方向向量
=(1,﹣1,2),直线m的方向向量![]() =(2,1,﹣
=(2,1,﹣![]() ),则l与m垂直;
),则l与m垂直;
②直线l的方向向量![]() =(0,1,﹣1),平面α的法向量
=(0,1,﹣1),平面α的法向量![]() =(1,﹣1,﹣1),则l⊥α;
=(1,﹣1,﹣1),则l⊥α;
③平面α、β的法向量分别为![]() =(0,1,3),
=(0,1,3),![]() =(1,0,2),则α∥β;
=(1,0,2),则α∥β;
④平面α经过三点A(1,0,﹣1),B(0,1,0),C(﹣1,2,0),向量![]() =(1,u,t)是平面α的法向量,则u+t=1.
=(1,u,t)是平面α的法向量,则u+t=1.
其中真命题的是______.(把你认为正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com