
【题目】已知函数![]() ,若
,若![]() 存在唯一的零点
存在唯一的零点![]() ,且
,且![]() ,则实数
,则实数![]() _______
_______
【答案】![]()
【解析】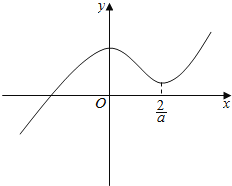
(i)当a=0时,f(x)=3x2+1,令f(x)=0,解得x=±![]() ,函数f(x)有两个零点,舍去。
,函数f(x)有两个零点,舍去。
(ii)当a≠0时,f′(x)=3ax26x=3ax(x![]() ),令f′(x)=0,解得x=0或2a.
),令f′(x)=0,解得x=0或2a.
①当a<0时, ![]() <0,当x<
<0,当x<![]() 或x>0时,f′(x)<0,此时函数f(x)单调递减;当
或x>0时,f′(x)<0,此时函数f(x)单调递减;当![]() <x<0时,f′(x)>0,此时函数f(x)单调递增。
<x<0时,f′(x)>0,此时函数f(x)单调递增。
∴![]() 是函数f(x)的极小值点,0是函数f(x)的极大值点。
是函数f(x)的极小值点,0是函数f(x)的极大值点。
∵函数f(x)=ax33x2+1存在唯一的零点x0,且x0<0,则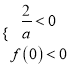 ,无解,舍去。
,无解,舍去。
②当a>0时, ![]() >0,当x>
>0,当x>![]() 或x<0时,f′(x)>0,此时函数f(x)单调递增;当0<x<
或x<0时,f′(x)>0,此时函数f(x)单调递增;当0<x<![]() 时,f′(x)<0,此时函数f(x)单调递减。
时,f′(x)<0,此时函数f(x)单调递减。
∴![]() 是函数f(x)的极小值点,0是函数f(x)的极大值点。
是函数f(x)的极小值点,0是函数f(x)的极大值点。
∵函数f(x)=ax33x2+1存在唯一的零点x0,且x0<0,则f(![]() >0,即
>0,即![]()
![]() +1>0,a>0,解得a>2.
+1>0,a>0,解得a>2.
综上可得:实数a的取值范围是(2,+∞).
故答案为:(2,+∞).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在投掷骰子试验中,根据向上的点数可以定义许多事件,如:A={出现1点},B={出现3点或4点},C={出现的点数是奇数},D={出现的点数是偶数}.
(1)说明以上4个事件的关系.
(2)求两两运算的结果.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人组成一个小组参加电视台举办的听曲猜歌名活动,在每一轮活动中,依次播放三首乐曲,然后甲猜第一首,乙猜第二首,丙猜第三首,若有一人猜错,则活动立即结束;若三人均猜对,则该小组进入下一轮,该小组最多参加三轮活动.已知每一轮甲猜对歌名的概率是![]() ,乙猜对歌名的概率是
,乙猜对歌名的概率是![]() ,丙猜对歌名的概率是
,丙猜对歌名的概率是![]() ,甲、乙、丙猜对与否互不影响.
,甲、乙、丙猜对与否互不影响.
(I)求该小组未能进入第二轮的概率;
(Ⅱ)记乙猜歌曲的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组: ![]() 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。

(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为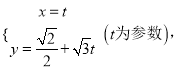 若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为
若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为![]()
(1)求直线![]() 的斜率和曲线C的直角坐标方程;
的斜率和曲线C的直角坐标方程;
(2)若直线![]() 与曲线C交于A、B 两点,设点
与曲线C交于A、B 两点,设点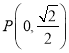 ,求|PA|+|PB|.
,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记X为比赛决出胜负时的总局数,求X的分布列和均值(数学期望).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com