
【题目】共享单车的出现方便了人们的出行,深受市民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)频率分布直方图.
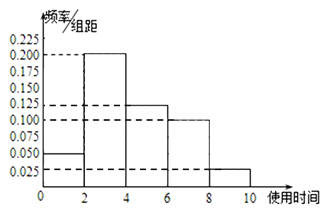
(1)已知该校大一学生有2400人,求抽取的100名学生中大一学生人数;
(2)根据频率分布直方图求该校大学生每周使用共享单车的平均时间.
(3)![]() 从抽取的100个样本中,用分层抽样的方法抽取使用共享单车时间超过6小时同学5人,再从这5人中任选2人,求这2人使用共享单车时间都不超过8小时的概率.
从抽取的100个样本中,用分层抽样的方法抽取使用共享单车时间超过6小时同学5人,再从这5人中任选2人,求这2人使用共享单车时间都不超过8小时的概率.
【答案】(1)30人;(2)4.4小时;(3)![]() .
.
【解析】试题分析:(1)首先根据根据抽取比例![]() ,然后再从2400人中按此比例抽取即可(2)取每个区间的中间值乘以对应的频率求和即为平均值(3)根据分层抽样根据(6,8],(8,10)的频率进行抽取可得使用共享单车时间在(6,8]小时内的有4人,记为A、B、C、D,在(8,10]小时内的有1人,然后写出基本事件找出满足条件的基本事件即可
,然后再从2400人中按此比例抽取即可(2)取每个区间的中间值乘以对应的频率求和即为平均值(3)根据分层抽样根据(6,8],(8,10)的频率进行抽取可得使用共享单车时间在(6,8]小时内的有4人,记为A、B、C、D,在(8,10]小时内的有1人,然后写出基本事件找出满足条件的基本事件即可
(1)设抽取的100名学生中大一学生有![]() 人,则,
人,则,![]() ,解得
,解得![]() ,
,
所以抽取的100名学生中大一学生有30人.
(2)![]()
![]() 所以该校大学生每周使用共享单车的平均时间大约为4.4小时.
所以该校大学生每周使用共享单车的平均时间大约为4.4小时.
(3)在100个样本中,任意抽取5人,使用共享单车时间在(6,8]小时内的有4人,记为A、B、C、D,在(8,10]小时内的有1人,记为X,从这5人任选2人的选法为:(A、B)、(A、C)、(A、D)、(A、X)、(B、C)、(B、D)、(B、X)、(C、D)、(C、X)、(D、X),共10中,其中这2人使用共享单车时间都不超过8小时的选法为(A、B)、(A、C)、(A、D)、(B、C)、(B、D)、(C、D),共6种,
所以,P=![]() .
.![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x+λ3﹣x(λ∈R).
(1)当λ=﹣4时,求函数f(x)的零点;
(2)若函数f(x)为偶函数,求实数λ的值;
(3)若不等式f(x)≤6在x∈[0,2]上恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义域为R上的奇函数,当x>0时,f(x)=x2+2x.
(1)求f(x)的解析式;
(2)若不等式f(t﹣2)+f(2t+1)>0成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在![]() 岁的问卷中随机抽取了
岁的问卷中随机抽取了![]() 份, 统计结果如下面的图表所示.
份, 统计结果如下面的图表所示.
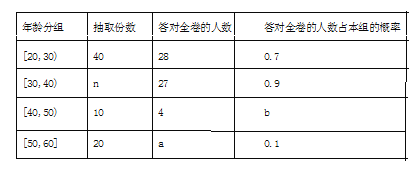
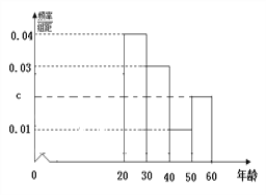
(1)分别求出![]() 的值;
的值;
(2)从年龄在![]() 答对全卷的人中随机抽取
答对全卷的人中随机抽取![]() 人授予“环保之星”,求年龄在
人授予“环保之星”,求年龄在![]() 的人中至少有
的人中至少有![]() 人被授予“环保之星”的概率.
人被授予“环保之星”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com