
【题目】如图,在底面为矩形的四棱锥![]() 中,
中, ![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
, ![]() ,
, ![]() ,求二面角
,求二面角![]() 的大小.
的大小.
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 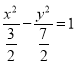
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)求证:函数y=x+ ![]() 有如下性质:如果常数a>0,那么该函数在(0,
有如下性质:如果常数a>0,那么该函数在(0, ![]() ]上是减函数,在[
]上是减函数,在[ ![]() ,+∞)上是增函数.
,+∞)上是增函数.
(2)若f(x)= ![]() ,x∈[0,1],利用上述性质,求函数f(x)的值域;
,x∈[0,1],利用上述性质,求函数f(x)的值域;
(3)对于(2)中的函数f(x)和函数g(x)=﹣x﹣2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1),求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄大点频率分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
|
频率 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:

(2)若对年龄在![]() 的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合A={x|(x﹣3)(x﹣a)=0,a∈R},B={x|(x﹣4)(x﹣1)=0},则集合A∪B,A∩B中元素的个数不可能是( )
A.4和1
B.4和0
C.3和1
D.3和0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆心为
是圆心为![]() 的圆
的圆![]() 上的动点,点
上的动点,点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)矩形![]() 的边所在直线与曲线
的边所在直线与曲线![]() 均相切,设矩形
均相切,设矩形![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E: ![]() (a>b>0),其长轴长是短轴长的
(a>b>0),其长轴长是短轴长的 ![]() 倍,过焦点且垂直于x轴的直线被椭圆截得的弦长为2
倍,过焦点且垂直于x轴的直线被椭圆截得的弦长为2 ![]() .
.
(1)求椭圆E的方程;
(2)设过右焦点F2且与x轴不垂直的直线l交椭圆E于P,Q两点,在线段OF2(O为坐标原点)上是否存在点M(m,0),使得以MP,MQ为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若集合A={x|kx2﹣2x﹣1=0}只有一个元素,则实数k的取值集合为( )
A.{﹣1}
B.{0}
C.{﹣1,0}
D.(﹣∞,﹣1]∪{0}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com