
����Ŀ��ijƷ�Ƶ��������Ԥ��ȫ�깺��![]() ̨���ԣ���֪��Ʒ�Ƶ��ԵĽ���Ϊ
̨���ԣ���֪��Ʒ�Ƶ��ԵĽ���Ϊ![]() Ԫ/̨��Ϊ��Լ�ʽ�����������룬��ÿ��������
Ԫ/̨��Ϊ��Լ�ʽ�����������룬��ÿ��������![]() ��
��![]() Ϊ��������̨����ÿ���踶�˷�
Ϊ��������̨����ÿ���踶�˷�![]() Ԫ�����湺��ĵ���ȫ���������ܷ���ÿ��������Ե��ܼ�ֵ�������˷ѣ������ȣ�����ϵ��Ϊ
Ԫ�����湺��ĵ���ȫ���������ܷ���ÿ��������Ե��ܼ�ֵ�������˷ѣ������ȣ�����ϵ��Ϊ![]() ������ÿ������
������ÿ������![]() ̨����ȫ���踶�˷Ѻͱ��ܷ�
̨����ȫ���踶�˷Ѻͱ��ܷ�![]() Ԫ.
Ԫ.
��1����ȫ�������˷Ѻͱ��ܷ�֮��Ϊ![]() Ԫ����
Ԫ����![]() ����
����![]() ���.
���.
��2����Ҫʹȫ������֧���˷Ѻͱ��ܷѵ��ʽ����٣���ÿ��Ӧ������Զ���̨��
���𰸡���1��![]() ����2��
����2��![]() ̨.
̨.
��������
��1����ÿ������![]() ̨������Ҫ����
̨������Ҫ����![]() �����ɼ�������˷Ѻ͵��Եı��ܷѣ��ɵó�
�����ɼ�������˷Ѻ͵��Եı��ܷѣ��ɵó�![]() ��ֵ����ÿ������
��ֵ����ÿ������![]() ̨������Ҫ����
̨������Ҫ����![]() ���������ɵó�
���������ɵó�![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2�����û�������ʽ���![]() ����Сֵ�����õȺų������������
����Сֵ�����õȺų������������![]() ��ֵ�����ɵý�.
��ֵ�����ɵý�.
��1����ÿ������![]() ̨������Ҫ����
̨������Ҫ����![]() �������˷�Ϊ
�������˷�Ϊ![]() Ԫ��
Ԫ��
ÿ��������Ե��ܼ�ֵΪ![]() Ԫ��������ɵ�
Ԫ��������ɵ�![]() ��
��
���![]() ��
��
��ÿ������![]() ̨������Ҫ����
̨������Ҫ����![]() ����
����
���ԣ�![]() ��
��
��2���ɻ�������ʽ�ɵ�![]() ��Ԫ����
��Ԫ����
���ҽ���![]() ʱ������
ʱ������![]() ʱ���Ⱥų���.
ʱ���Ⱥų���.
��ˣ���ÿ������![]() ̨����ʱ��ȫ������֧���˷Ѻͱ��ܷѵ��ʽ�����.
̨����ʱ��ȫ������֧���˷Ѻͱ��ܷѵ��ʽ�����.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
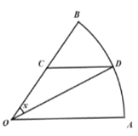
����Ŀ��Ϊ��ףijУһ������У�죬չʾ��Уһ�������İ�ѧ�ɹ�������У�ѷ�ɣ�ѧУ��У���ڼ�һ������չ��������ͼ����һ���뾶Ϊ2������Բ�Ľ�Ϊ![]() ������չʾ����ƽ��ʾ��ͼ.��
������չʾ����ƽ��ʾ��ͼ.��![]() �ǰ뾶
�ǰ뾶![]() ��һ�㣬��
��һ�㣬��![]() ��Բ��
��Բ��![]() ��һ�㣬��
��һ�㣬��![]() .Ϊ��ʵ�֡���չ��չ�����־��������߶�
.Ϊ��ʵ�֡���չ��չ�����־��������߶�![]() ���߶�
���߶�![]() ��Բ��
��Բ��![]() ������ʾλ���������λ����������λ���������ǣ��߶�
������ʾλ���������λ����������λ���������ǣ��߶�![]() ��ÿ����Ϊ
��ÿ����Ϊ![]() Ԫ���߶�
Ԫ���߶�![]() ��Բ��
��Բ��![]() ��ÿ������Ϊ
��ÿ������Ϊ![]() Ԫ.��
Ԫ.��![]() ���ȣ����λ�����������Ϊ
���ȣ����λ�����������Ϊ![]() Ԫ.
Ԫ.
��1����![]() ����
����![]() �ĺ�������ʽ����ָ���ú����Ķ�����
�ĺ�������ʽ����ָ���ú����Ķ�����
��2������![]() Ϊ��ֵʱ�����λ����������������������ֵ.
Ϊ��ֵʱ�����λ����������������������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ,��Բ��������Ϊ
,��Բ��������Ϊ![]() ,����Բ
,����Բ![]() ����
����![]() ,��б��Ϊ
,��б��Ϊ![]() ��ֱ��
��ֱ��![]() ,�����ҽ���
,�����ҽ���![]() ΪԲ��,�뾶Ϊ
ΪԲ��,�뾶Ϊ![]() ��Բ
��Բ![]() ����.
����.
��1������Բ![]() �ı�����;
�ı�����;
��2���߶�![]() ����Բ
����Բ![]() ���ҽ���
���ҽ���![]() ����,��
����,��![]() ,��
,��![]() ����������ֵ�Լ�ȡ���ֵʱʵ��
����������ֵ�Լ�ȡ���ֵʱʵ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ������
������![]() Ϊ������λ���������⸴��
Ϊ������λ���������⸴��![]() ����
����![]() ��
��![]() ��
��
��1����![]() ��ֵ��
��ֵ��
��2��������![]() ����
����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3�����ǰ�������ϵʽ������ƽ���ϱ�ʾ����![]() �ĵ�
�ĵ�![]() �ͱ�ʾ����
�ͱ�ʾ����![]() �ĵ�
�ĵ�![]() ֮���һ���任�����Ƿ����һ��ֱ��
֮���һ���任�����Ƿ����һ��ֱ��![]() ������
������![]() ��ֱ��
��ֱ��![]() �ϣ����
�ϣ����![]() ��Ȼ��ֱ��
��Ȼ��ֱ��![]() �ϣ�������ڣ����ֱ��
�ϣ�������ڣ����ֱ��![]() �ķ��̣�����˵�����ɣ�
�ķ��̣�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����
������![]() �IJ���������
�IJ���������![]() ��
��![]() ��������������
Ϊ��������������![]() ����������Ϊԭ����
����������Ϊԭ����![]() ������������Ϊԭ����һ�룬�õ�����
������������Ϊԭ����һ�룬�õ�����![]() ��ֱ��
��ֱ��![]() ����ͨ������
����ͨ������![]() ��������ԭ��
��������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ��������Ϊ���Ὠ��������ϵ��
��������Ϊ���Ὠ��������ϵ��
��1����ֱ��![]() �ļ����귽�̺�����
�ļ����귽�̺�����![]() ����ͨ���̣�
����ͨ���̣�
��2��������![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ���ڼ���ֵ�뼫Сֵ������
���ڼ���ֵ�뼫Сֵ������![]() ��ȡ�ü�Сֵ.
��ȡ�ü�Сֵ.
��1����ʵ��![]() ��ֵ��
��ֵ��
��2��������![]() ��������㣬��ʵ��
��������㣬��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���ο����ݣ�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̼Һ���4500��Ԫ����һ��![]() ��������ʵ���豸�������Ժ�ƻ����꿪ʼͶ��ʹ�ã������豸��ĺ�ά������һ����ά�ޱ�������200��Ԫ���ӵڶ��꿪ʼ��ÿ���ά�ޱ������ñ���һ����40��Ԫ.���豸ʹ�ú�ÿ���������Ϊ2800��Ԫ.
��������ʵ���豸�������Ժ�ƻ����꿪ʼͶ��ʹ�ã������豸��ĺ�ά������һ����ά�ޱ�������200��Ԫ���ӵڶ��꿪ʼ��ÿ���ά�ޱ������ñ���һ����40��Ԫ.���豸ʹ�ú�ÿ���������Ϊ2800��Ԫ.
(1)��ӯ����![]() ����Ԫ����ʹ������
����Ԫ����ʹ������![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
(2)���豸ʹ�ö����꣬�̼ҵ���ƽ��ӯ������������ƽ��ӯ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֻ������ǵ��������������ͬʱ��Ҳ��������ijɳ�����������Ӱ�죬���˳������ֻ���Ϸ���Σ�����Ӱ�����Լ���ѧҵ��ijѧУ�����ȡ![]() ���࣬���������ֻ���ѧУ���������������ݵľ�Ҷͼ��ͼ��ʾ�������Ϊ
���࣬���������ֻ���ѧУ���������������ݵľ�Ҷͼ��ͼ��ʾ�������Ϊ![]() �����ݷ����
�����ݷ����![]() ��
��![]() ������
������![]() ��
��![]() ʱ��������Ƶ�ʷֲ�ֱ��ͼ�ǣ� ��
ʱ��������Ƶ�ʷֲ�ֱ��ͼ�ǣ� ��

A.  B.
B. 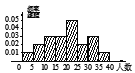
C. 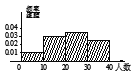 D.
D. 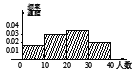
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC��x2+y2+2x��4y+3��0��
��1����ֱ��l��x+y��0��ԲC����A��B���㣬����AB�ij���
��2����ԲC��һ��P��x1��y1�����Բ��һ�����ߣ��е�ΪM��OΪ����ԭ�㣬����|PM|��|PO|����ʹ��|PM|ȡ����Сֵ�ĵ�P�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com